一、单选题 (共 26 题,每小题 5 分,共 50 分,每题只有一个选项正确)
设 $f(x)=\arcsin x$, 则 $f^{\prime \prime}(0)$ 为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ -1
设 $f(x)=\left\{\begin{array}{l}\frac{2}{3} x^3, x \leq 1 \\ x^2, x>1\end{array}\right.$, 则 $f(x)$ 在 $x=1$ 处的
$\text{A.}$ 左、右导数都存在
$\text{B.}$ 左导数存在, 右导数不存在
$\text{C.}$ 左导数不存在, 右导数存在
$\text{D.}$ 左、右导数都不存在
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内单调有界, $\left\{x_n\right\}$ 为数列, 下列命题正确的是
$\text{A.}$ 若 $\left\{x_n\right\}$ 收敛, 则 $\left\{f\left(x_n\right)\right\}$ 收敛
$\text{B.}$ 若 $\left\{x_n\right\}$ 单调,则 $\left\{f\left(x_n\right)\right\}$ 收敛
$\text{C.}$ 若 $\left\{f\left(x_n\right)\right\}$ 收敛, 则 $\left\{x_n\right\}$ 收敛.
$\text{D.}$ 若 $\left\{f\left(x_n\right)\right\}$ 单调, 则 $\left\{x_n\right\}$ 收敛.
函数 $f(x)=\lim _{n \rightarrow \infty} \frac{x^n+2}{x^n+1}$ 的间断点及类型是
$\text{A.}$ $x=1$ 是第一类间断点, $x=-1$ 是第二类间断点
$\text{B.}$ $x=1$ 是第二类间断点, $x=-1$ 是第一类间断点
$\text{C.}$ $x=\pm 1$ 均是第一类间断点
$\text{D.}$ $x=\pm 1$ 均是第二类间断点
当 $x \rightarrow 0^{+}$时, 与 $\sqrt{x}$ 等价的无穷小量是
$\text{A.}$ $1-\mathrm{e}^{\sqrt{x}}$.
$\text{B.}$ $\sqrt{1+\sqrt{x}}-1$.
$\text{C.}$ $\ln \frac{1+x}{1-\sqrt{x}}$.
$\text{D.}$ $1-\cos \sqrt{x}$.
设函数 $f(x)$ 在 $x=0$ 处连续, 下列命题错误的是
$\text{A.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)}{x}$ 存在, 则 $f(0)=0$.
$\text{B.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)+f(-x)}{x}$ 存在, 则 $f(0)=0$.
$\text{C.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)}{x}$ 存在, 则 $f^{\prime}(0)$ 存在.
$\text{D.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)-f(-x)}{x}$ 存在, 则 $f^{\prime}(0)$ 存在.
曲线 $y=x \ln \left(\mathrm{e}+\frac{1}{x}\right) \quad(x>0)$ 的渐近线条数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设 $F(x)=\int_x^{x+2 \pi} \mathrm{e}^{\sin t} \sin t \mathrm{~d} t$, 则 $F(x)$
$\text{A.}$ 为正常数
$\text{B.}$ 为负常数
$\text{C.}$ 恒为零.
$\text{D.}$ 不为常数
设随机变量 $X$ 的密度函数为 $f(x)=\frac{2}{\pi} \sqrt{1-x^2}, x \in(-1,1)$. 对任意 $x \in(-1,1)$,若在条件 $X=x$ 下, 随机变量 $Y$ 的条件分布律为
$$
\mathrm{P}\left(Y=-\sqrt{1-x^2}\right)=\mathrm{P}\left(Y=\sqrt{1-x^2}\right)=1 / 2,
$$
则 $Y$ ________ 连续型随机变量, $(X, Y)$ ________ 连续型随机向量.
$\text{A.}$ 是, 是
$\text{B.}$ 是, 不是
$\text{C.}$ 不是, 是
$\text{D.}$ 不是, 不是
设 $X_1, X_2, \cdots, X_n$ 为一列独立同分布的随机变量, 且均服从参数为 $\lambda>0$ 的指数分布. 记 $\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i$ 且 $\Phi(x)$ 为标准正态分布函数, 则对任意 $x \in \mathbb{R}$, 有
$\text{A.}$ $\lim _{n \rightarrow \infty} \mathrm{P}\left(\frac{\sqrt{n}}{\lambda}(\bar{X}-\lambda) \leq x\right)=\Phi(x)$
$\text{B.}$ $\lim _{n \rightarrow \infty} \mathrm{P}\left(\sqrt{\frac{n}{\lambda}}(\bar{X}-\lambda) \leq x\right)=\Phi(x)$
$\text{C.}$ $\lim _{n \rightarrow \infty} \mathrm{P}(\sqrt{n}(\lambda \bar{X}-1) \leq x)=\Phi(x)$
$\text{D.}$ $\lim _{n \rightarrow \infty} \mathrm{P}\left(\sqrt{n \lambda}\left(\bar{X}-\frac{1}{\lambda}\right) \leq x\right)=\Phi(x)$
设 $X_1, X_2, \cdots, X_n$ 是来自正态总体 $N\left(\mu, \sigma^2\right)$ 的简单随机样本, 其中 $\mu$ 为已知常数,记 $\bar{X}$ 和 $S^2$ 分别为样本均值和样本方差, 则下列统计量中与 $\bar{X}$ 不独立的是
$\text{A.}$ 样本标准差
$\text{B.}$ $\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2$
$\text{C.}$ $\frac{1}{n} \sum_{i=1}^n\left(X_i-\mu\right)^2$
$\text{D.}$ $X_1-X_2$
设 $X_1, X_2, X_3$ 是来自正态总体 $N\left(\mu, \sigma^2\right)$ 的简单随机样本, 则下列统计量中, ( ) 为 $\mu$ 的无偏估计且方差最小.
$\text{A.}$ $\frac{1}{2} X_1+\frac{1}{3} X_2+\frac{1}{6} X_3$
$\text{B.}$ $\frac{1}{3} X_1+\frac{1}{3} X_2+\frac{1}{3} X_3$
$\text{C.}$ $\frac{1}{5} X_1+\frac{2}{5} X_2+\frac{2}{5} X_3$
$\text{D.}$ $\frac{1}{7} X_1+\frac{2}{7} X_2+\frac{3}{7} X_3$
假设检验中, 在显著性水平 $\alpha=0.05$ 下若原假设 $H_0$ 被接受, 这说明
$\text{A.}$ 有充分的理由表明 $H_0$ 是正确的
$\text{B.}$ 没有充分的理由表明 $H_0$ 是错误的
$\text{C.}$ 有充分的理由表明 $H_1$ 是错误的
$\text{D.}$ 没有充分的理由表明 $H_1$ 是正确的
设当${x\rightarrow0}$时,${e^{x}-\left(ax^{2}+bx+1\right)}$是比${x^2}$高阶的无穷小,则 .
$\text{A.}$ $a=\frac{1}{2},b=1$
$\text{B.}$ $a=1,b=1$
$\text{C.}$ $a=-\frac{1}{2},b=-1$
$\text{D.}$ $a=-1,b=1$
设函数 $f(x)=|x|$, 则函数在点 $x=0$ 处
$\text{A.}$ 连续且可导
$\text{B.}$ 连续且可微
$\text{C.}$ 连续不可导
$\text{D.}$ 不连续不可微
$x=0$ 是函数 $f(x)=\arctan \frac{1}{x}$ 的
$\text{A.}$ 可去间断点
$\text{B.}$ 跳跃间断点
$\text{C.}$ 连续点
$\text{D.}$ 无穷间断点
函数 $f(x)$ 的定义域为 $(a, b)$, 导函数 $f^{\prime}(x)$ 在 $(a, b)$ 内的图像如图所示, 则函数 $f(x)$ 在 $(a, b)$ 内有极小值点
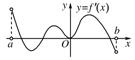
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
若 $\int f(x) d x=F(x)+C$, 则 $\int f(2 x+3) d x=$
$\text{A.}$ $F(2 x+3)$
$\text{B.}$ $2 F(2 x+3)+\mathrm{C}$
$\text{C.}$ $\frac{1}{2} F(2 x+3)$
$\text{D.}$ $\frac{1}{2} F(2 x+3)+C$
函数 $f(x)$ 在 $[a, b]$ 上连续是 $f(x)$ 在 $[a, b]$ 上可积的
$\text{A.}$ 充要条件
$\text{B.}$ 必要条件
$\text{C.}$ 充分条件
$\text{D.}$ 非必要非充分条件
下列反常积分发散的是
$\text{A.}$ $\int_1^{+\infty} \frac{1}{x^2} d x$
$\text{B.}$ $\int_0^1 \frac{x d x}{\sqrt{1-x^2}}$
$\text{C.}$ $\int_0^1 \frac{1}{\sqrt{x}} d x$
$\text{D.}$ $\int_1^{+\infty} \frac{1}{x \ln x} d x$
设函数 $f(x)$ 在 $(-\infty,+\infty)$ 内单调有界, $\left\{x_n\right\}$ 为数列, 下列命题正确的是
$\text{A.}$ 若 $\left\{x_n\right\}$ 收敛, 则 $\left\{f\left(x_n\right)\right\}$ 收敛
$\text{B.}$ 若 $\left\{x_n\right\}$ 单调, 则 $\left\{f\left(x_n\right)\right\}$ 收敛
$\text{C.}$ 若 $\left\{f\left(x_n\right)\right\}$ 收敛, 则 $\left\{x_n\right\}$ 收敛.
$\text{D.}$ 若 $\left\{f\left(x_n\right)\right\}$ 单调, 则 $\left\{x_n\right\}$ 收敛.
函数 $f(x)=\lim _{n \rightarrow \infty} \frac{x^n+2}{x^n+1}$ 的间断点及类型是
$\text{A.}$ $x=1$ 是第一类间断点, $x=-1$ 是第二类间断点
$\text{B.}$ $x=1$ 是第二类间断点, $x=-1$ 是第一类间断点
$\text{C.}$ $x= \pm 1$ 均是第一类间断点
$\text{D.}$ $x= \pm 1$ 均是第二类间断点
当 $x \rightarrow 0^{+}$时, 与 $\sqrt{x}$ 等价的无穷小量是
$\text{A.}$ $1-\mathrm{e}^{\sqrt{x}}$.
$\text{B.}$ $\sqrt{1+\sqrt{x}}-1$.
$\text{C.}$ $\ln \frac{1+x}{1-\sqrt{x}}$.
$\text{D.}$ $1-\cos \sqrt{x}$.
设函数 $f(x)$ 在 $x=0$ 处连续, 下列命题错误 的是
$\text{A.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)}{x}$ 存在, 则 $f(0)=0$.
$\text{B.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)+f(-x)}{x}$ 存在, 则 $f(0)=0$.
$\text{C.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)}{x}$ 存在, 则 $f^{\prime}(0)$ 存在.
$\text{D.}$ 若 $\lim _{x \rightarrow 0} \frac{f(x)-f(-x)}{x}$ 存在, 则 $f^{\prime}(0)$ 存在.
曲线 $y=x \ln \left(\mathrm{e}+\frac{1}{x}\right) \quad(x>0)$ 的渐近线条数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设 $F(x)=\int_x^{x+2 \pi} \mathrm{e}^{\sin t} \sin t \mathrm{~d} t$, 则 $F(x)$
$\text{A.}$ 为正常数.
$\text{B.}$ 为负常数.
$\text{C.}$ 恒为零.
$\text{D.}$ 不为常数.
二、填空题 (共 10 题, 每小题 5 分,共 20 分, 请把答案直接填写在答题纸上)
设函数 $f(x)$ 的定义域 $D=[0,4]$, 则函数 $f\left(x^2\right)$ 的定义域是
极限 $\lim _{x \rightarrow 1} \frac{x^3-1}{x-1}=$
极限 $\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}=$
曲线 $y=\frac{x^2}{9 x^2-1}$ 的水平渐近线方程为
若 $x^2-a \sin x$ 和 $x$ 是 $x \rightarrow 0$ 时的等价无穷小, 则 $a=$.
曲线 $y=\arctan \frac{1}{x}$ 在点 $\left(1, \frac{\pi}{4}\right)$ 的切线方程为
函数 $f(x)=\frac{\ln x}{x^2}$ 的导数 $f^{\prime}(x)=$.
若 $f(x)=x(x+1)(x+2)(x+3) \cdots(x+2021)$, 则 $f^{\prime}(0)=$
曲线$y=(x-5)x^{\frac{2}{3}}$的拐点坐标为$\_\_\_\_\_$.
$\lim _{x \rightarrow 0} \frac{1}{x}\left(\frac{1}{\sin x}-\frac{1}{\tan x}\right)=$
三、解答题 ( 共 4 题,满分 80 分,解答过程应写出必要的文字说明、证明过程或演算步骤 )
设 $f^{\prime \prime}(x)$ 在 $[0,2]$ 上连续且 $\left|f^{\prime \prime}(x)\right| \leq M, f(1)=0$, 证明: $\left|\int_0^2 f(x) \mathrm{d} x\right| \leq \frac{M}{3}$.
设 $\left\{\begin{array}{l}x=1+t^2 \\ y=1+t^3\end{array}\right.$, 求 $\frac{d y}{d x}, \frac{d^2 y}{d x^2}$.
求函数 $y=\ln \left(x^2+1\right)$ 的图形的拐点和凹凸区间
要制作一个体积为 $V$ 的圆柱形无盖铁桶, 问如何确定其底面半径和高才能用料最省?