一、单选题 (共 6 题,每小题 3 分,共 18 分,每题只有一个选项正确)
设 $f(x)=\arcsin x$, 则 $f^{\prime \prime}(0)$ 为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ -1
设 $f(x)=\left\{\begin{array}{l}\frac{2}{3} x^3, x \leq 1 \\ x^2, x>1\end{array}\right.$, 则 $f(x)$ 在 $x=1$ 处的
$\text{A.}$ 左、右导数都存在
$\text{B.}$ 左导数存在, 右导数不存在
$\text{C.}$ 左导数不存在, 右导数存在
$\text{D.}$ 左、右导数都不存在
曲线 $y=x \ln \left(\mathrm{e}+\frac{1}{x}\right) \quad(x>0)$ 的渐近线条数为
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设 $F(x)=\int_x^{x+2 \pi} \mathrm{e}^{\sin t} \sin t \mathrm{~d} t$, 则 $F(x)$
$\text{A.}$ 为正常数
$\text{B.}$ 为负常数
$\text{C.}$ 恒为零.
$\text{D.}$ 不为常数
$x=0$ 是函数 $f(x)=\arctan \frac{1}{x}$ 的
$\text{A.}$ 可去间断点
$\text{B.}$ 跳跃间断点
$\text{C.}$ 连续点
$\text{D.}$ 无穷间断点
函数 $f(x)$ 的定义域为 $(a, b)$, 导函数 $f^{\prime}(x)$ 在 $(a, b)$ 内的图像如图所示, 则函数 $f(x)$ 在 $(a, b)$ 内有极小值点
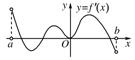
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
二、计算题 (共 5 题, 每小题 8分,共 40 分, 请把答案直接填写在答题纸上)
确定常数 $b$, 使得直线 $y=9 x+b$ 为曲线 $y=x^3-3 x$ 的切线;
求极限 $\lim _{x \rightarrow+\infty} \frac{\ln \left(x^2+3 x+1\right)}{\ln \left(x^3+2 x+1\right)}$;
求函数 $f(x)=(x+1) \ln (x+1)$ 的单调区间和极值;
求不定积分 $\int \frac{x}{\sqrt{4-x^4}} \mathrm{~d} x$;
设 $f(x)=\left\{\begin{array}{ll}x, & 0 \leq x \leq 1 \\ 2-x, & 1 < x,\end{array}\right.$ 求 $\int_2^4 f(x-2) \mathrm{e}^{-x} \mathrm{~d} x$;