单选题 （共 15 题 ），每题只有一个选项正确
设全集 $I=\{1,2,3,4,5,6,7\}$, 集合 $A=\{1,3,5,7\}, B=\{3,5\}$. 则
$\text{A.}$ $I=A \cup B$
$\text{B.}$ $I=\bar{A} \mathrm{U} B$
$\text{C.}$ $I=A \mathrm{U} \bar{B}$
$\text{D.}$ $I=\bar{A} \mathrm{U} \bar{B}$
当 $a>1$ 时, 在同一坐标系中, 函数 $y=a^{-x}$ 与 $y=\log _a x$ 的图像
$\text{A.}$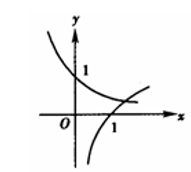 
$\text{B.}$ 
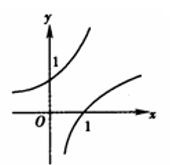$\text{C.}$ 
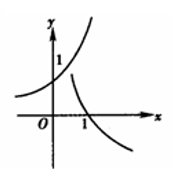$\text{D.}$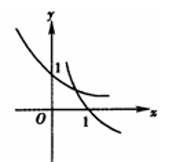 
若 $\sin ^2 x>\cos ^2 x$, 则 $x$ 的取值范围是
$\text{A.}$ $\left\{x \left\lvert\, 2 k \pi-\frac{3}{4} \pi < x < 2 k \pi+\frac{1}{4} \pi\right., k \in \mathbf{Z}\right\}$
$\text{B.}$ $\left\{x \left\lvert\, 2 k \pi+\frac{1}{4} \pi < x < 2 k \pi+\frac{5}{4} \pi\right., k \in \mathbf{Z}\right\}$
$\text{C.}$ $\left\{x \left\lvert\, k \pi-\frac{1}{4} \pi < x < k \pi+\frac{1}{4} \pi\right., k \in \mathbf{Z}\right\}$
$\text{D.}$ $\left\{x \left\lvert\, k \pi+\frac{1}{4} \pi < x < k \pi+\frac{3}{4} \pi\right., k \in \mathbf{Z}\right\}$
复数 $\frac{(2+2 i)^4}{(1-\sqrt{3} i)^5}$ 等于
$\text{A.}$ $1+\sqrt{3} i$
$\text{B.}$ $-1+\sqrt{3} i$
$\text{C.}$ $1-\sqrt{3} i$
$\text{D.}$ $-1-\sqrt{3} i$
6 名同学排成一排，其中甲、乙两人必须排在一起的不同排法有
$\text{A.}$ 720 种
$\text{B.}$ 360 种
$\text{C.}$ 240 种
$\text{D.}$ 120 种
已知 $\alpha$ 是第三象限角且 $\sin \alpha=-\frac{24}{25}$, 则 $\tan \frac{\alpha}{2}=$
$\text{A.}$ $\frac{4}{3}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $-\frac{3}{4}$
$\text{D.}$ $-\frac{4}{3}$
如果直线 $l, m$ 与平面 $\alpha, \beta, \gamma$ 满足: $l=\beta \mathrm{I} \gamma, l / / \alpha, m \subset \alpha$ 和 $m \perp \gamma$, 那么必有
$\text{A.}$ $\alpha \perp \gamma$ 且 $l \perp m$
$\text{B.}$ $\alpha \perp \gamma$ 且 $m / / \beta$
$\text{C.}$ $m / / \beta$ 且 $l \perp m$
$\text{D.}$ $\alpha / / \beta$ 且 $\alpha \perp \gamma$
当 $-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$ 时,函数 $f(x)=\sin x+\sqrt{3} \cos x$ 的
$\text{A.}$ 最大值是 1 , 最小值是 -1
$\text{B.}$ 最大值是 1 , 最小值是 $-\frac{1}{2}$
$\text{C.}$ 最大值是 2 , 最小值是 -2
$\text{D.}$ 最大值是 2 , 最小值是 -1
中心在原点, 准线方程为 $x= \pm 4$, 离心率为 $\frac{1}{2}$ 的椭圆方程是
$\text{A.}$ $\frac{x^2}{4}+\frac{y^2}{3}=1$
$\text{B.}$ $\frac{x^2}{3}+\frac{y^2}{4}=1$
$\text{C.}$ $\frac{x^2}{4}+y^2=1$
$\text{D.}$ $x^2+\frac{y^2}{4}=1$
圆锥母线长为 1 , 侧面展开图圆心角为 $240^{\circ}$, 该圆锥的体积是
$\text{A.}$ $\frac{2 \sqrt{2} \pi}{81}$
$\text{B.}$ $\frac{8 \pi}{81}$
$\text{C.}$ $\frac{4 \sqrt{5} \pi}{81}$
$\text{D.}$ $\frac{10 \pi}{81}$
椭圆 $25 x^2-150 x+9 y^2+18 y+9=0$ 的两个焦点坐标是
$\text{A.}$ $(-3,5),(-3,-3)$
$\text{B.}$ $(3,3),(3,-5)$
$\text{C.}$ $(1,1),(-7,1)$
$\text{D.}$ $(7,-1),(-1,-1)$
将边长为 $a$ 的正方形 $A B C D$ 沿对角线 $A C$ 折起, 使得 $B D=a$, 则三棱锥 $D-A B C$ 的体积为
$\text{A.}$ $\frac{a^3}{6}$
$\text{B.}$ $\frac{a^3}{12}$
$\text{C.}$ $\frac{\sqrt{3}}{12} a^3$
$\text{D.}$ $\frac{\sqrt{2}}{12} a^3$
等差数列 $\left\{a_n\right\}$ 的前 $m$ 项和为 30 , 前 $2 m$ 项和为 100 , 则它的前 $3 m$ 项和为
$\text{A.}$ 130
$\text{B.}$ 170
$\text{C.}$ 210
$\text{D.}$ 260
设双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(0 < a < b)$ 的半焦距为 $c$, 直线 $l$ 过 $(a, 0),(0, b)$ 两点. 已知原点到直线 $l$ 的距离为 $\frac{\sqrt{3}}{4} c$, 则双曲线的离心率为
$\text{A.}$ 2
$\text{B.}$ $\sqrt{3}$
$\text{C.}$ $\sqrt{2}$
$\text{D.}$ $\frac{2 \sqrt{3}}{3}$
$f(x)$ 是 $(-\infty,+\infty)$ 上的奇函数, $f(x+2)=-f(x)$, 当 $0 \leq x \leq 1$ 时, $f(x)=x$, 则 $f(7.5)$ 等于
$\text{A.}$ 0.5
$\text{B.}$ -0.5
$\text{C.}$ 1.5
$\text{D.}$ -1.5
填空题 （共 4 题 ），请把答案直接填写在答题纸上
已知点 $(-2,3)$ 与抛物线 $y^2=2 p x(p>0)$ 的焦点的距离是 5 , 则 $p=$
正六边形的中心和顶点共 7 个点, 以其中 3 个点为顶点的三角形共有 $\qquad$个. (用数字作答)
$\operatorname{tg} 20^{\circ}+\operatorname{tg} 40^{\circ}+\sqrt{3} \operatorname{tg} 20^{\circ} \operatorname{tg} 40^{\circ}$ 的值是
19. 如图, 正方形 $A B C D$ 所在平面与正方形 $A B E F$ 所在平面成 $60^{\circ}$ 的二面角, 则异面直线 $A D$ 与 $B F$ 所成角的余弦值是
解答题 （共 6 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
设等比数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$. 若 $S_3+S_6=2 S_9$, 求数列的公比 $q$.
已知 $\triangle A B C$ 的三个内角 $A, B, C$ 满足: $A+C=2 B, \frac{1}{\cos A}+\frac{1}{\cos C}=-\frac{\sqrt{2}}{\cos B}$, 求 $\cos \frac{A-C}{2}$ 的值.
某地现有耕地 10000 公顷，规划 10 年后粮食单产比现在增加 $22 \%$, 人均粮食占有量比现在提高 $10 \%$. 如果人口年增长率为 $1 \%$, 那么耕地平均每年至多只能减少多少公顷（精确到 1 公顷）?
（粮食单产 $=\frac{\text { 总产量 }}{\text { 耕地面积 }}$, 人均粮食占有量 $=\frac{\text { 总产量 }}{\text { 总人口数 }}$ )
已知 $l_1, l_2$ 是过点 $P(-\sqrt{2}, 0)$ 的两条互相垂直的直线, 且 $l_1, l_2$ 与双曲线 $y^2-x^2=1$ 各有两个交点, 分别为 $A_1, B_1$ 和 $A_2, B_2$.
( I ) 求 $l_1$ 的斜率 $k_1$ 的取值范围;
( II ) 若 $A_1$ 恰是双曲线的一个顶点, 求 $\left|A_2 B_2\right|$ 的值.
已知 $a 、 b 、 c$ 是实数, 函数 $f(x)=a x^2+b x+c, g(x)=a x+b$, 当 $-1 \leqslant x \leqslant 1$ 时, $|f(x)| \leqslant 1$.
( I ) 证明: $|\mathrm{c}| \leqslant 1$ ；
(II) 证明: 当 $-1 \leqslant x \leqslant 1$ 时, $|g(x)| \leqslant 2$;
(III) 设 $a>0$, 当 $-1 \leqslant x \leqslant 1$ 时, $g(x)$ 的最大值为 2 , 求 $f(x)$.