一、单选题 (共 15 题 ),每题只有一个选项正确
1. 已知 , 并且 是第二象限的角, 那么 的值等于
2. 焦点在 , 顶点在 的抛物线方程是
3. 函数 的最小正周期是
4. 如果把两条异面直线看成 “一对”, 那么六棱锥的棱所在的 12 条直线中, 异面直线共有
12对
24对
36对
48对
5. 函数 的图像的一条对称轴的方程是
6. 如果三棱锥 的底面是不等边三角形, 侧面与底面所成的二面角都相等, 且顶点 在底面的射影 O 在 内, 那么 O 是 的
垂心
重心
外心
内心
7. 已知 是等比数列, 且 , 那么 的值等于
5
10
15
20
8. 如果圆锥曲线的极坐标方程为 , 那么它的焦点的极坐标为
9. 从 4 台甲型和 5 台乙型电视机中任意取出 3 台, 其中至少要有甲型与乙型电视机各 1 台,则不同的取法共有
140种
84 种
70 种
35 种
10. 如果 且 , 那么直线 不通过
第一象限
第二象限
第三象限
第四象限
11. 设甲、乙、丙是三个命题. 如果甲是乙的必要条件; 丙是乙的充分条件但不是乙的必要条件, 那么
丙是甲的充分条件, 但不是甲的必要条件
丙是甲的必要条件, 但不是甲的充分条件
丙是甲的充要条件
丙不是甲的充分条件, 也不是甲的必要条件
12. 的值等于
0
1
2
3
13. 如果奇函数 在区间 上是增函数且最小值为 5 , 那么 在区间 , 上是
增函数且最小值为一 5
增函数且最大值为 -5
减函数且最小值为 -5
减函数且最大值为 -5
14. 圆 上到直线 的距离为 的点共有
1 个
2 个
3 个
4 个
15. 设全集为R, , 那么集合 等于
二、填空题 (共 5 题 ),请把答案直接填写在答题纸上
16. 的值是
18. 已知正三棱台上底面边长为 2 , 下底面边长为 4 , 且侧棱与底面所成的角是 ,那么这个正三棱台的体积等于
19. 的展开式中, 的系数是 的系数与 的系数的等差中项. 若实数 , 那么
20. 在球面上有四个点 、、、, 如果 、、 两两互相垂直, 且 . 那么这个球面的面积是
三、解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
21. 设 , 在复数集 中解方程 .
22. 求函数 的最小值,并写出使函数 取最小值的 的集合.
23. 已知复数 , 求复数 的模和辐角的主值.
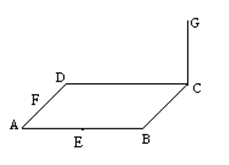
24. 已知
是边长为 4 的正方形,
、 分别是
、 的中点,
垂直于
所在的平面, 且
. 求点
到平面
的距离.
25. 根据函数单调性的定义, 证明函数 在 上是减函数.
26. 已知 为自然数, 实数 , 解关于 的不等式
27. 双曲线的中心在坐标原点 , 焦点在 轴上, 过双曲线右焦点且斜率为 的直线交双曲线于 、 两点. 若 , 求双曲线的方程.
28. 设 是等差数列, . 已知 . 求等差数列的通项 .
29. 设 , 解关于 的不等式 .
30. 已知椭圆的中心在坐标原点 , 焦点在坐标轴上, 直线 与该椭圆相交于 和 ,且 . 求椭圆的方程.