一、单选题 (共 12 题 ),每题只有一个选项正确
1. 实数 - 5 的相反数是
2. 下列计算正确的是()
3. 下列整式中, 是二次单项式的是()
4. 天问一号于 2020 年 7 月 23 日在文昌航天发射场由长征五号遥四运 载火筧发射升空, 于 2021 年 5 月 15 日在火星成功着陆, 总飞行里程超过 450000000 千 米. 数据 450000000 用科学记数法表示为()
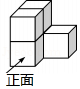
5. 如图是由5个大小相同的小正方体组成的几何体,则它的主视图是
6. 在一个不透明的袋中装有 5 个球, 其中 2 个红球, 3 个白球, 这些 球除颜色外无其他差别, 从中随机摸出 1 个球, 摸出红球的概率是()
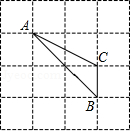
7. 如图, 点
、、 都在方格纸的格点上, 若点
的坐标为
, 点
的坐标为
, 则点
的坐标是
8. 用配方法解方程 , 配方后所得的方程是()
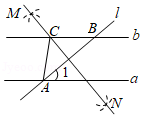
9. 如图, 已知
, 直线
与直线
、 分别交于点
、, 分别以点
、 为圆心, 大于
的长为半径画弧, 两弧相交于点
、, 作直线
, 交直线
于点
, 连接
, 若
, 则
的度数是 ( )
10. 如图, 四边形
是
的内接四边形,
是
的直径, 连 接
. 若
, 则
的度数是()

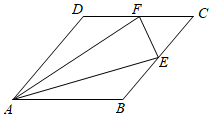
11. 如图, 在菱形
中, 点
、 分别是边
、 的中点, 连 接
、、. 若菱形
的面积为 8, 则
的面积为()
2
3
4
5
12. 李叔叔开车上班, 最初以某一速度匀速行驶, 中途停车加油耽误 了几分钟, 为了按时到单位, 李叔叔在不违反交通规则的前提下加快了速度, 仍保持匀 速行驶, 则汽车行驶的路程 (千米) 与行驶的时间 (小时) 的函数关系的大致图象是 ()
二、填空题 (共 10 题 ),请把答案直接填写在答题纸上
14. 若点 在反比例函数 的图象上, 则 (填 ">" " < " 或"=")
15. 如图,
的顶点
、 的坐标分别是
、, 且
, 则顶点
的坐标是
16. 如图, 在矩形 中, , 将此矩形折叠, 使点 与点 重合, 点 落在点 处, 折痕为 , 则 的长为 ———— 的长为 ————
17. (1)计算:
;
(2)解不等式组
并把它的解集在数轴(如图)上表示出来.
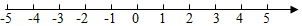
18. 为了庆祝中国共产党成立 100 周年, 某校组织了党史知识竞赛, 学校购买了若干副乒乓球拍
和羽毛球拍对表现优异的班级进行奖励. 若购买 2 副乒乓球拍和 1 副羽毛球拍共需 280
元; 若购买 3 副乒乓球拍和 2 副羽毛球拍共需 480 元. 求 1 副乒乓球拍和 1 副羽毛球拍
各是多少元?
19. 根据 2021 年 5 月 11 日国务院新闻办公室发布的《第七次全国人口普查公报》, 就我国 2020年每 10 万人中, 拥有大学 (指大专及以上)、高中 (含中专)、初中、小学、其他等文化 程度的人口(以上各种受教育程度的人包括各类学校的毕业生、肄业生和在校生)受教 育情况数据, 绘制了条形统计图 (图 1) 和扇形统计图 (图 2).
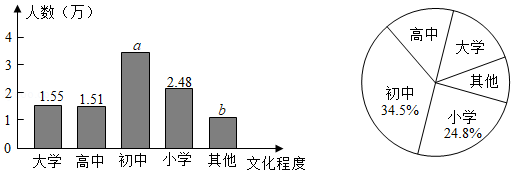
根据统计图提供的信息, 解答下列问题:
(1)
,
(2) 在第六次全国人口普查中, 我国 2010 年每 10 万人中拥有大学文化程度的人数约为
万, 则 2020 年每 10 万人中拥有大学文化程度的人数与 2010 年相比, 增长率是 (精确到
).
(3) 2020 年海南省总人口约 1008 万人, 每 10 万人中拥有大学文化程度的人数比全国每 10 万人中拥有大学文化程度的人数约少
万, 那么全省拥有大学文化程度的人数约有 万(精确到 1 万).
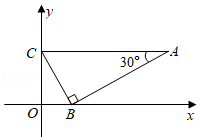
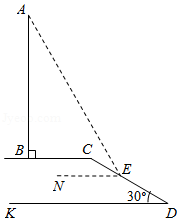
20. 如图, 在某信号塔
的正前方有一斜坡
, 坡角
, 斜坡的顶端
与塔底
的距离
米, 小明在斜坡上的点
处测得塔顶
的仰角
米, 且
(点
在同一平面内).
(1) 填空:
度,
度;
(2) 求信号塔的高度
(结果保留根号).
21. 如图 1, 在正方形
中, 点
是边
上一点, 且点
不与点
、 重合, 点
是
的延长线上一点, 且
.
(1) 求证:
;
(2) 如图 2, 连接
, 交
于点
, 过点
作
, 垂足为
, 延长
交
于点
, 连接
.
(1)求证:
;
(2) 若
, 求
的长.

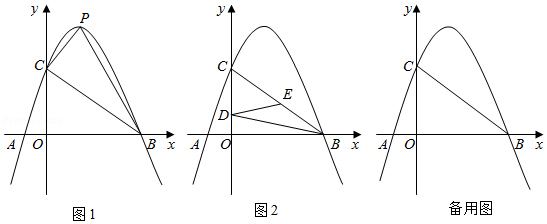
22. 已知抛物线
与
轴交于
、 两点, 与
轴交于
点, 具点
的坐标为
,
、点
的坐标为
.
(1) 求该抛物线的函数表达式;
(2) 如图 1, 若该抛物线的顶点为
, 求
的面积;
(3) 如图 2, 有两动点
、 在
的边上运动, 速度均为每秒 1 个单位长度, 它们 分别从点
和点
同时出发, 点
沿折线
按
方向向终点
运动, 点
沿线段
按
方向向终点
运动, 当其中一个点到达终点时, 另一个点也随之停止 运动. 设运动时间为
秒, 请解答下列问题:
(1)当
为何值时,
的面积等于
;
(2)在点
、 运动过程中, 该抛物线上存在点
, 使得依次连接
、、、 得到 的四边形
是平行四边形, 请直接写出所有符合条件的点
的坐标.