已知抛物线 $y=a x^{2}+\frac{9}{4} x+c$ 与 $x$ 轴交于 $A 、 B$ 两点, 与 $y$ 轴交于 $C$ 点, 具点 $A$ 的坐标为 $(-1$,$0)$ 、点 $C$ 的坐标为 $(0,3)$.
(1) 求该抛物线的函数表达式;
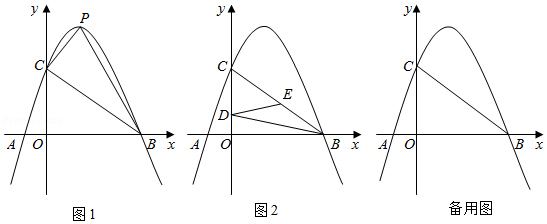
(2) 如图 1, 若该抛物线的顶点为 $P$, 求 $\triangle P B C$ 的面积;
(3) 如图 2, 有两动点 $D 、 E$ 在 $\triangle C O B$ 的边上运动, 速度均为每秒 1 个单位长度, 它们 分别从点 $C$ 和点 $B$ 同时出发, 点 $D$ 沿折线 $C O B$ 按 $C \rightarrow O \rightarrow B$ 方向向终点 $B$ 运动, 点 $E$ 沿线段 $B C$ 按 $B \rightarrow C$ 方向向终点 $C$ 运动, 当其中一个点到达终点时, 另一个点也随之停止 运动. 设运动时间为 $t$ 秒, 请解答下列问题:
(1)当 $t$ 为何值时, $\triangle B D E$ 的面积等于 $\frac{33}{10}$;
(2)在点 $D 、 E$ 运动过程中, 该抛物线上存在点 $F$, 使得依次连接 $A D 、 D F 、 F E 、 E A$ 得到 的四边形 $A D F E$ 是平行四边形, 请直接写出所有符合条件的点 $F$ 的坐标.
(1) 求该抛物线的函数表达式;
(2) 如图 1, 若该抛物线的顶点为 $P$, 求 $\triangle P B C$ 的面积;
(3) 如图 2, 有两动点 $D 、 E$ 在 $\triangle C O B$ 的边上运动, 速度均为每秒 1 个单位长度, 它们 分别从点 $C$ 和点 $B$ 同时出发, 点 $D$ 沿折线 $C O B$ 按 $C \rightarrow O \rightarrow B$ 方向向终点 $B$ 运动, 点 $E$ 沿线段 $B C$ 按 $B \rightarrow C$ 方向向终点 $C$ 运动, 当其中一个点到达终点时, 另一个点也随之停止 运动. 设运动时间为 $t$ 秒, 请解答下列问题:
(1)当 $t$ 为何值时, $\triangle B D E$ 的面积等于 $\frac{33}{10}$;
(2)在点 $D 、 E$ 运动过程中, 该抛物线上存在点 $F$, 使得依次连接 $A D 、 D F 、 F E 、 E A$ 得到 的四边形 $A D F E$ 是平行四边形, 请直接写出所有符合条件的点 $F$ 的坐标.
