已知实数 $x, y, z$, 满足 $y+z-2=0$, 则 $\sqrt{x^2+y^2+z^2}+\sqrt{(x-2)^2+y^2+z^2}+\sqrt{(x-1)^2+y^2+(z-2)^2}+\sqrt{(x-1)^2+(y-2)^2+z^2}$ 的最小值为

如图, 在四棱椎 $P-A B C D$ 中, 底面 $A B C D$ 是边长为 2 的菱形, $\angle B A D=60^{\circ}, M$ 是侧棱 $P C$ 的中点, 侧面 $P A D$ 为正三角形, 侧面 $P A D \perp$ 底面 $A B C D$.

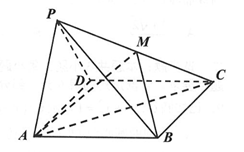
(1) 求三棱椎 $M-A B C$ 的体积;
(2) 求 $A M$ 与平面 $P B C$ 所成角的正弦值.

已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的右焦点为 $F$, 左顶点为 $A$, 短轴长为 $2 \sqrt{3}$, 且经过点 $\left(1, \frac{3}{2}\right)$.
(1) 求椭圆 $C$ 的方程;
(2) 过点 $F$ 的直线 $l$ (不与 $x$ 轴重合) 与 $C$ 交于 $P, Q$ 两点, 直线 $A P, A Q$ 与直线 $x=4$ 的交点分别为 $M, N$,记直线 $M F, N F$ 的斜率分别为 $k_1, k_2$, 证明: $k_1 \cdot k_2$ 为定值.

树人中学高三（1）班某次数学质量检测（满分150分）的统计数据如下表：

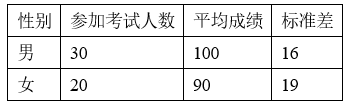
在按比例分配分层随机抽样中, 已知总体划分为 2 层, 把第一层样本记为 $x_1, x_2, x_3, \mathrm{~L}, x_n$, 其平均数记为 $\bar{x}$,方差记为 $s_1^2$; 把第二层样本记为 $y_1, y_2, y_3, \mathrm{~L}, y_m$, 其平均数记为 $\bar{y}$, 方差记为 $s_2^2$; 把总样本数据的平均数记为 $\bar{z}$, 方差记为 $s^2$.
(1) 证明: $s^2=\frac{1}{m+n}\left\{n\left[s_1^2+(\bar{x}-\bar{z})^2\right]+m\left[s_2^2+(\bar{y}-\bar{z})^2\right]\right\}$;
(2) 求该班参加考试学生成绩的平均数和标准差 (精确到 1);
（3）假设全年级学生的考试成绩服从正态分布 $N\left(\mu, \sigma^2\right)$, 以该班参加考试学生成绩的平均数和标准差分别作为 $\mu$ 和 $\sigma$ 的估计值. 如果按照 $16 \%, 34 \%, 34 \%, 16 \%$ 的比例将考试成绩从高分到低分依次划分为 $A, B, C, D$ 四个等级, 试确定各等级的分数线 (精确到 1 ).
附: $P(\mu-\sigma \leq X \leq \mu+\sigma) \approx 0.68, \sqrt{302} \approx 17, \sqrt{322} \approx 18, \sqrt{352} \approx 19$.

已知曲线 $C: f(x)=\mathrm{e}^x-x \mathrm{e}^x$ 在点 $A(1, f(1))$ 处的切线为 $l$.
(1) 求直线 $l$ 的方程;
(2) 证明: 除点 $A$ 外，曲线 $C$ 在直线 $l$ 的下方;
(3) 设 $f\left(x_1\right)=f\left(x_2\right)=t, x_1 \neq x_2$, 求证: $x_1+x_2 < 2 t-\frac{t}{\mathrm{e}}-1$.

在数学中, 广义距离是泛函分析中最基本的概念之一. 对平面直角坐标系中两个点 $P_1\left(x_1, y_1\right)$ 和 $P_2\left(x_2, y_2\right)$,记
$$
\left|P_1 P_2\right|_t=\max \left\{\frac{\left|x_1-x_2\right|}{1+\left|x_1-x_2\right|}, \frac{\left|y_1-y_2\right|}{1+\left|y_1-y_2\right|}\right\},
$$
称 $\left|P_1 P_2\right|_t$ 为点 $P_1$ 与点 $P_2$ 之间的 “ $t$-距离”, 其中 $\max \{p, q\}$ 表示 $p, q$ 中较大者.
(1) 计算点 $P(1,2)$ 和点 $Q(2,4)$ 之间的 “ $t$ - 距离” ;
(2) 设 $P_0\left(x_0, y_0\right)$ 是平面中一定点, $r>0$. 我们把平面上到点 $P_0$ 的 “ $t$-距离” 为 $r$ 的所有点构成的集合叫做以点 $P_0$ 为圆心, 以 $r$ 为半径的 “ $t$-圆” . 求以原点 $O$ 为圆心, 以 $\frac{1}{2}$ 为半径的 “ $t$ - 圆” 的面积;
(3) 证明: 对任意点 $P_1\left(x_1, y_1\right), P_2\left(x_2, y_2\right), P_3\left(x_3, y_3\right),\left|P_1 P_3\right|_t \leq\left|P_1 P_2\right|_t+\left|P_2 P_3\right|_t$.