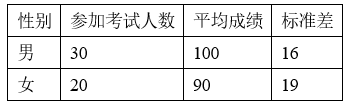
树人中学高三（1）班某次数学质量检测（满分150分）的统计数据如下表：

在按比例分配分层随机抽样中, 已知总体划分为 2 层, 把第一层样本记为 $x_1, x_2, x_3, \mathrm{~L}, x_n$, 其平均数记为 $\bar{x}$,方差记为 $s_1^2$; 把第二层样本记为 $y_1, y_2, y_3, \mathrm{~L}, y_m$, 其平均数记为 $\bar{y}$, 方差记为 $s_2^2$; 把总样本数据的平均数记为 $\bar{z}$, 方差记为 $s^2$.
(1) 证明: $s^2=\frac{1}{m+n}\left\{n\left[s_1^2+(\bar{x}-\bar{z})^2\right]+m\left[s_2^2+(\bar{y}-\bar{z})^2\right]\right\}$;
(2) 求该班参加考试学生成绩的平均数和标准差 (精确到 1);
（3）假设全年级学生的考试成绩服从正态分布 $N\left(\mu, \sigma^2\right)$, 以该班参加考试学生成绩的平均数和标准差分别作为 $\mu$ 和 $\sigma$ 的估计值. 如果按照 $16 \%, 34 \%, 34 \%, 16 \%$ 的比例将考试成绩从高分到低分依次划分为 $A, B, C, D$ 四个等级, 试确定各等级的分数线 (精确到 1 ).
附: $P(\mu-\sigma \leq X \leq \mu+\sigma) \approx 0.68, \sqrt{302} \approx 17, \sqrt{322} \approx 18, \sqrt{352} \approx 19$.