单选题 （共 8 题 ），每题只有一个选项正确
计算: $3-5=$
$\text{A.}$ $2$
$\text{B.}$ $-2$
$\text{C.}$ $8$
$\text{D.}$ $-82$
下列图形中，既是轴对称图形，又是中心对称图形的是
$\text{A.}$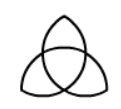 
$\text{B.}$ 
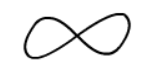$\text{C.}$ 
$\text{D.}$ 
如图， $l / / A B ， \angle A=2 \angle B$ ，若 $\angle 1=108^{\circ}$ ，则 $\angle 2$ 的度数为
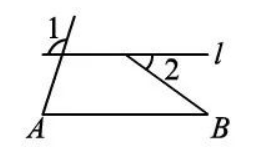
$\text{A.}$ $36^{\circ}$
$\text{B.}$ $46^{\circ}$
$\text{C.}$ $72^{\circ}$
$\text{D.}$ $82^{\circ}$
计算: $6 x y^2 \cdot\left(-\frac{1}{2} x^3 y^3\right)=$
$\text{A.}$ $3 x^4 y^5$
$\text{B.}$ $-3 x^4 y^5$
$\text{C.}$ $3 x^3 y^6$
$\text{D.}$ $-3 x^3 y^6$
在同一平面直角坐标系中，函数 $y=a x$ 和 $y=x+a(a$ 为常数， $a < 0)$ 的图象可能是
$\text{A.}$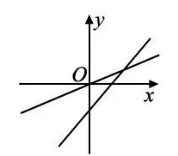 
$\text{B.}$ 
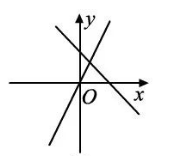$\text{C.}$ 
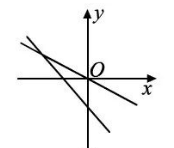$\text{D.}$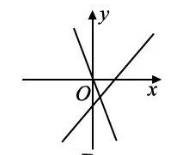 
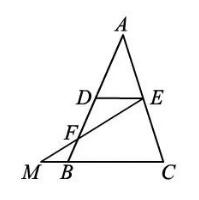
如图， $D E$ 是 $\triangle A B C$ 的中位线，点 $F$ 在 $D B$ 上， $D F=2 B F$ ，连接 $E F$ 并延长，与 $C B$ 的延长线相交于点 $M$. 若 $B C=6$, 则线段 $C M$ 的长为
$\text{A.}$ $\frac{13}{2}$
$\text{B.}$ 7
$\text{C.}$ $\frac{15}{2}$
$\text{D.}$ 8
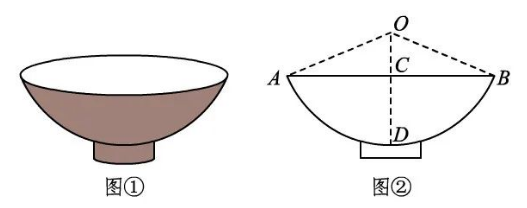
陕西饮食文化源远流长，“老碗面”是陕西地方特色美食之一. 图 (2) 是从正面看到的一个“老碗”(图 (1) ) 的形状示意图， $\widehat{A B}$ 是 $\odot O$ 的一部分， $D$ 是 $\widehat{A B}$ 的中点，连接 $O D ，$与弦 $A B$ 交于点 $C$ ，连接 $O A, O B$. 已知 $A B=24 \mathrm{~cm}$ ，碗深 $C D=8 \mathrm{~cm}$ ，则 $\odot O$ 的半径 $O A$ 为
$\text{A.}$ 13cm
$\text{B.}$ 16cm
$\text{C.}$ 17cm
$\text{D.}$ 26cm
在平面直角坐标系中, 二次函数 $y=x^2+m x+m^2-m$ ( $m$ 为常数)的图像经过点 $(0,6)$ ，其对称轴在轴左侧，则该二次函数有
$\text{A.}$ 最大值 5
$\text{B.}$ 最大值 $\frac{15}{4}$
$\text{C.}$ 最小值 5
$\text{D.}$ 最小值 $\frac{15}{4}$
填空题 （共 5 题 ），请把答案直接填写在答题纸上
如图，在数轴上，点A表示 $\sqrt{3}$ ，点 $B$ 与点 $A$ 位于原点的两侧，且与原点的距离相等，则点 $B$ 表示的数是
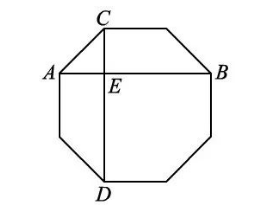
如图, 正八边形的边长为 2 ，对角线 $A B 、 C D$ 相交于 $E$ ，则线段 $B E$ 的长为
点 $E$ 是菱形 $A B C D$ 的对称中心， $\angle B=56^{\circ}$ ，连接 $A E$ ，则 $\angle B A E$ 的度数为
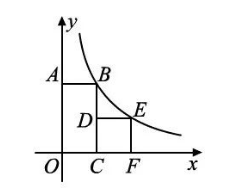
如图, 在矩形 $O A B C$ 和正方形 $C D E F$ 中，点 $A$ 在 $y$ 轴正半轴上，点 $C 、 F$ 均在 $x$ 轴正半轴上，点 $D$ 在边 $B C$ 上， $B C=2 C D, A B=3$. 若点 $B 、 E$ 在同一个反比例函数的图象上，则这个反比例函数的表达式是
如图,在矩形 $A B C D$ 中， $A B=3, B C=4$, 点 $E$ 在边 $A D$ 上，且 $E D=3$ ， $M 、 N$ 分别是边 $A B 、 B C$ 上的动点，且 $B M=B N ， P$ 是线段 $C E$ 上的动点，连接 $P M ， P N$ ，若 $P M+P N=4$, 则线段 $P C$ 的长为
解答题 （共 13 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式： $\frac{3 x-5}{2}>2 x$.
计算:$\sqrt{5} \times(-\sqrt{10})-\left(\frac{1}{7}\right)^{-1}+\left|-2^3\right| .$
化简:$\left(\frac{3 a}{a^2-1}-\frac{1}{a-1}\right) \div \frac{2 a-1}{a+1} .$
如图，一锐角 $\triangle A B C ， \angle B=48^{\circ}$ ，请用尺规作图法，在 $\triangle A B C$ 内部求作一点 $P$ ，使 $P B=P C$ ，且 $\angle P B C=24^{\circ}$. (保留作图痕迹，不写作法)
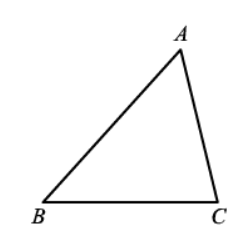
如图，在 $\triangle A B C$ 中， $\angle B=50^{\circ} ， \angle C=20^{\circ}$. 过点 $A$ 作 $A E \perp B C$ ，垂足为 $E$ ，延长 $E A$ 至点 $D$ ，使 $A D=A C$ ，在边 $A C$ 上截取 $A F=A B$ ，连接 $D F$.
求证: $D E=C B$.
一个不透明的袋子中装有四个小球，这四个小球上各标有一个数. 分别是 $1 ， 1 ， 2$ ， 3 . 这些小球除标有的数字外都相间.
(1)从袋中随机摸出一个小球，则摸出的这个小球上标有的数字是 1 的概率率为
(2)先从袋中随机摸出一个小球，记下小球上标有的数字后，放回，摇匀，再从袋中随机摸出一个小球, 记下小球上标有的数字. 请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率.
小红在一家文具店买了一种大笔记本 4 个和一种小笔记本 6 个，共用了 62 元. 已知她买的这种大笔记本的单价比这种小笔记本的单价多 3 元. 求该文具店中这种大笔记本的单价.
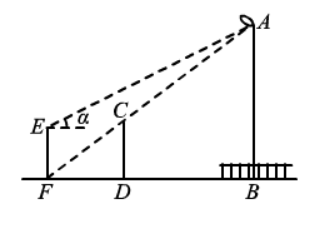
一天晚上，小明和爸爸带着测角仪和皮尺区公园测量一景观灯 (灯杆底部不可到达)的高 $A B$. 如图所示，当小明爸爸站在点 $D$ 处时，他在该景观灯照射下的影子长为 $D F$ ，测得 $D F=2.4 m$ ；当小明站在爸爸影子的顶端 $F$ 处时，测得点 $A$ 的仰角 $\alpha$ 为 $26.6^{\circ}$.已知爸爸的身高 $C D=1.8 m$ ，小明眼睛到地面的距离 $E F=1.6 m$ ，点 $F 、 D$ 、 $B$ 在同一条直线上, $E F \perp F B, C D \perp F B, A B \perp F B$. 求该景观灯的高 $A B$. (参考数据: $\sin 26.6^{\circ} \approx 0.45, \cos 26.6^{\circ} \approx 0.89, \tan 26.6^{\circ} \approx 0.50$ )
经验表明，树在一定的成长阶段，其胸径(树的主干在地面以上 $1.3 \mathrm{~m}$ 处的直径)越大，树就越高. 通过对某种树进行测量研究，发现这种树的树高 $y(m)$ 是其胸径 $x(m)$ 的一次函数. 已知这种树的胸径为 $0.2 m$ 时，树高为 $20 m$; 这种树的胸径为 $0.28 m$ 时，树高为 $22 m$.
(1)求 $y$ 与 $x$ 之间的函数表达式;
(2)当这种树的胸径为 0.3 时，其树高是多少?
某校数学兴趣小组的同学们从“校园农场”中随机抽取了 20 棵西红柿植株，并统计了每棵植株上小西红柿的个数. 其数据如下:通过对以上数据的分析整理，绘制了如下统计图表:
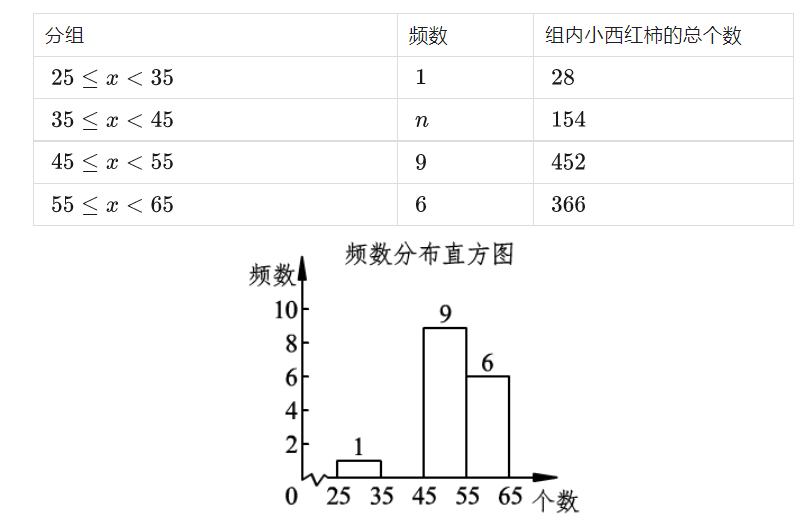
根据以上信息，解答下列问题:
(1)补全频数分布直方图; 这 20 个数据的众数是
(2)求这 20 个数据的平均数;
(3)“校园农场”中共有 300 棵这种西红柿植株，请估计这 300 棵西红柿植株上小西红柿的总个数.
如图， $\triangle A B C$ 内接于 $\odot O ， \angle B A C=45^{\circ}$ ，过点 $B$ 作 $B C$ 的垂线，交 $\odot O$ 于点 $D$ ，并于 $C A$ 的延长线交于点 $E$ ，作 $B F \perp A C$ ，垂足为 $M$ ，交 $\odot O$ 于点 $F$.
(1)求证: $B D=B C$;
(2)若 $\odot O$ 的半径 $r=3, B E=6$, 求线段 $B F$ 的长.
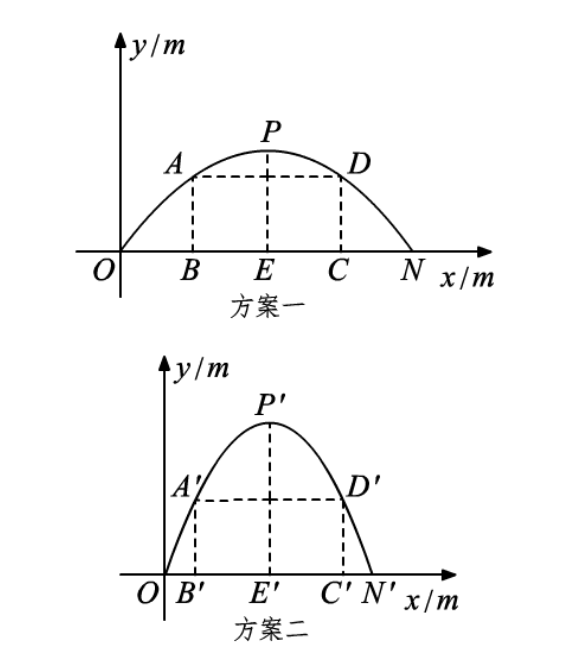
某校想将新建图书楼的正门设计为一个抛物线型拱门, 并要求所设计的拱门的跨度与拱高之积为 $48 \mathrm{~m}^2$, 还要兼顾美观、大方、和谐、通畅等因素, 设计部门按要求给出了两个设计方案. 现把这两个方案中的拱门图形放入平面直角坐标系中, 如图所示:
方案一. 抛物线型拱门的跨度 $O N=12 m$ ，拱高 $P E=4 m$. 其中，点 $N$ 在 $x$ 轴上, $P E \perp O N, O E=E N$.
方案二. 抛物线型拱门的跨度 $O N^{\prime}=8 m$ ，拱高 $P^{\prime} E^{\prime}=6 m$. 其中，点 $N^{\prime}$ 在 $x$轴上, $P^{\prime} E^{\prime} \perp O N^{\prime}, O E^{\prime}=E^{\prime} N^{\prime}$.
要在拱门中设置高为 $3 m$ 的矩形框架, 其面积越大越好(框架的粗细忽略不计). 方案一中，矩形框架 $A B C D$ 的面积为 $S_1$ ，点 $A 、 D$ 在抛物线上,边 $B C$ 在 $O N$ 上; 方案二中, 矩形框架 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 的面积为 $S_2$ ，点 $A^{\prime} 、 D^{\prime}$ 在抛物线上，边 $B^{\prime} C^{\prime}$ 在 $O N^{\prime}$上.
现知，小华已正确求出方案二中，当 $A^{\prime} B^{\prime}=3 m$ 时， $S_2=12 \sqrt{2} m^2$.
请你根据以上提供的相关信息, 解答下列问题:
(1)求方案一中抛物线的函数表达式;
(2)在方案一中，当 $A B=3 m$ 时，求矩形框架 $A B C D$ 的面积 $S_1$ ，并比较 $S_1 ， S_2$的大小.
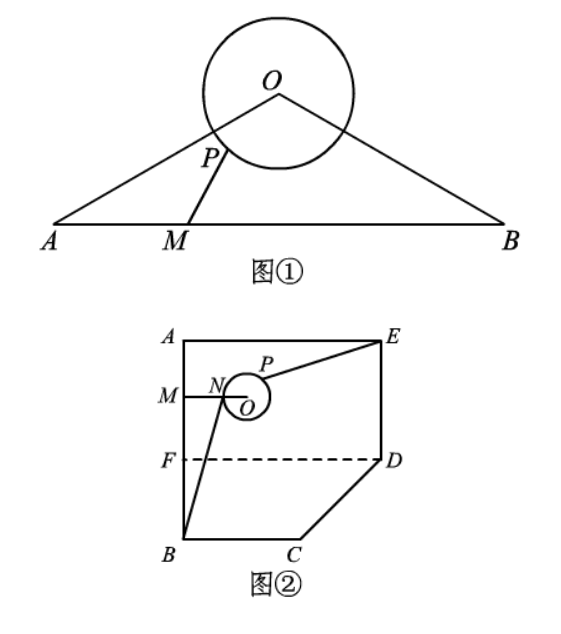
(1)如图 ①，在 $\triangle O A B$ 中， $O A=O B ， \angle A O B=120^{\circ} ， A B=24$ ，若 $\odot O$的半径为 4 ，点 $\mathrm{P}$ 在 $\odot O$ 上，点 $\mathrm{M}$ 在 $A B$ 上，连接 $P M$ ，求线段 $P M$ 的最小值.
(2)如图② 所示, 五边形 $\mathrm{ABCDE}$ 是某市工业新区的外环路, 新区管委会在点 $\mathrm{B}$ 处, 点 $\mathrm{E}$处是该市的一个交通枢纽. 已知: $\angle A=\angle A B C=\angle A E D=90^{\circ}, A B=A E=$ $10000 \mathrm{~m} . B C=D E=6000 \mathrm{~m}$. 根据新区的自然环境及实际需求, 现要在矩形 $A F D E$ 区域内 (含边界) 修一个半径为 $30 \mathrm{~m}$ 的圆形环道 $\odot O$ ；过圆心 $O$ ，作 $O M \perp A B$ ，垂足为 $M$ ，与 $\odot O$ 交于点 $N$ ，连接 $B N$. 点 $P$ 在 $\odot O$ 上，连接 $E P$.其中，线段 $B N 、 E P$ 及 $M N$ 是要修的三条道路, 要在所修道路 $B N 、 E P$ 之和最短的情况下，使所修道路 $M N$ 最短，试求此时环道 $\odot O$ 的圆心 $O$ 到 $A B$ 的距离 $O M$的长.
