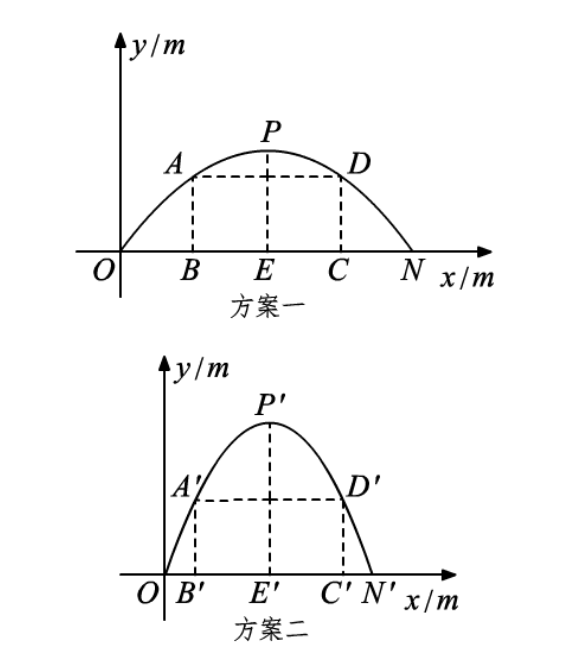
某校想将新建图书楼的正门设计为一个抛物线型拱门, 并要求所设计的拱门的跨度与拱高之积为 $48 \mathrm{~m}^2$, 还要兼顾美观、大方、和谐、通畅等因素, 设计部门按要求给出了两个设计方案. 现把这两个方案中的拱门图形放入平面直角坐标系中, 如图所示:
方案一. 抛物线型拱门的跨度 $O N=12 m$ ,拱高 $P E=4 m$. 其中,点 $N$ 在 $x$ 轴上, $P E \perp O N, O E=E N$.
方案二. 抛物线型拱门的跨度 $O N^{\prime}=8 m$ ,拱高 $P^{\prime} E^{\prime}=6 m$. 其中,点 $N^{\prime}$ 在 $x$轴上, $P^{\prime} E^{\prime} \perp O N^{\prime}, O E^{\prime}=E^{\prime} N^{\prime}$.
要在拱门中设置高为 $3 m$ 的矩形框架, 其面积越大越好(框架的粗细忽略不计). 方案一中,矩形框架 $A B C D$ 的面积为 $S_1$ ,点 $A 、 D$ 在抛物线上,边 $B C$ 在 $O N$ 上; 方案二中, 矩形框架 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 的面积为 $S_2$ ,点 $A^{\prime} 、 D^{\prime}$ 在抛物线上,边 $B^{\prime} C^{\prime}$ 在 $O N^{\prime}$上.
现知,小华已正确求出方案二中,当 $A^{\prime} B^{\prime}=3 m$ 时, $S_2=12 \sqrt{2} m^2$.
请你根据以上提供的相关信息, 解答下列问题:
(1)求方案一中抛物线的函数表达式;
(2)在方案一中,当 $A B=3 m$ 时,求矩形框架 $A B C D$ 的面积 $S_1$ ,并比较 $S_1 , S_2$的大小.
方案一. 抛物线型拱门的跨度 $O N=12 m$ ,拱高 $P E=4 m$. 其中,点 $N$ 在 $x$ 轴上, $P E \perp O N, O E=E N$.
方案二. 抛物线型拱门的跨度 $O N^{\prime}=8 m$ ,拱高 $P^{\prime} E^{\prime}=6 m$. 其中,点 $N^{\prime}$ 在 $x$轴上, $P^{\prime} E^{\prime} \perp O N^{\prime}, O E^{\prime}=E^{\prime} N^{\prime}$.
要在拱门中设置高为 $3 m$ 的矩形框架, 其面积越大越好(框架的粗细忽略不计). 方案一中,矩形框架 $A B C D$ 的面积为 $S_1$ ,点 $A 、 D$ 在抛物线上,边 $B C$ 在 $O N$ 上; 方案二中, 矩形框架 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 的面积为 $S_2$ ,点 $A^{\prime} 、 D^{\prime}$ 在抛物线上,边 $B^{\prime} C^{\prime}$ 在 $O N^{\prime}$上.

现知,小华已正确求出方案二中,当 $A^{\prime} B^{\prime}=3 m$ 时, $S_2=12 \sqrt{2} m^2$.
请你根据以上提供的相关信息, 解答下列问题:
(1)求方案一中抛物线的函数表达式;
(2)在方案一中,当 $A B=3 m$ 时,求矩形框架 $A B C D$ 的面积 $S_1$ ,并比较 $S_1 , S_2$的大小.