(1)如图 ①,在 $\triangle O A B$ 中, $O A=O B , \angle A O B=120^{\circ} , A B=24$ ,若 $\odot O$的半径为 4 ,点 $\mathrm{P}$ 在 $\odot O$ 上,点 $\mathrm{M}$ 在 $A B$ 上,连接 $P M$ ,求线段 $P M$ 的最小值.
(2)如图② 所示, 五边形 $\mathrm{ABCDE}$ 是某市工业新区的外环路, 新区管委会在点 $\mathrm{B}$ 处, 点 $\mathrm{E}$处是该市的一个交通枢纽. 已知: $\angle A=\angle A B C=\angle A E D=90^{\circ}, A B=A E=$ $10000 \mathrm{~m} . B C=D E=6000 \mathrm{~m}$. 根据新区的自然环境及实际需求, 现要在矩形 $A F D E$ 区域内 (含边界) 修一个半径为 $30 \mathrm{~m}$ 的圆形环道 $\odot O$ ;过圆心 $O$ ,作 $O M \perp A B$ ,垂足为 $M$ ,与 $\odot O$ 交于点 $N$ ,连接 $B N$. 点 $P$ 在 $\odot O$ 上,连接 $E P$.其中,线段 $B N 、 E P$ 及 $M N$ 是要修的三条道路, 要在所修道路 $B N 、 E P$ 之和最短的情况下,使所修道路 $M N$ 最短,试求此时环道 $\odot O$ 的圆心 $O$ 到 $A B$ 的距离 $O M$的长.
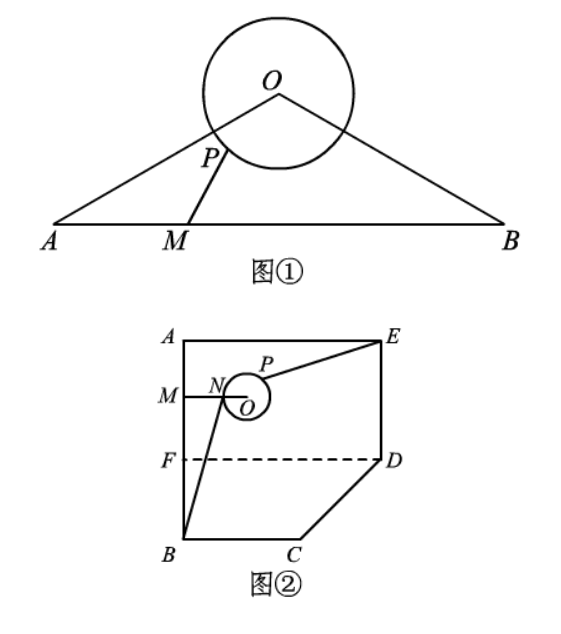
(2)如图② 所示, 五边形 $\mathrm{ABCDE}$ 是某市工业新区的外环路, 新区管委会在点 $\mathrm{B}$ 处, 点 $\mathrm{E}$处是该市的一个交通枢纽. 已知: $\angle A=\angle A B C=\angle A E D=90^{\circ}, A B=A E=$ $10000 \mathrm{~m} . B C=D E=6000 \mathrm{~m}$. 根据新区的自然环境及实际需求, 现要在矩形 $A F D E$ 区域内 (含边界) 修一个半径为 $30 \mathrm{~m}$ 的圆形环道 $\odot O$ ;过圆心 $O$ ,作 $O M \perp A B$ ,垂足为 $M$ ,与 $\odot O$ 交于点 $N$ ,连接 $B N$. 点 $P$ 在 $\odot O$ 上,连接 $E P$.其中,线段 $B N 、 E P$ 及 $M N$ 是要修的三条道路, 要在所修道路 $B N 、 E P$ 之和最短的情况下,使所修道路 $M N$ 最短,试求此时环道 $\odot O$ 的圆心 $O$ 到 $A B$ 的距离 $O M$的长.
