单选题 (共 12 题 ),每题只有一个选项正确
-5 的相反数是
$\text{A.}$ $-\frac{1}{5}$
$\text{B.}$ $\frac{1}{5}$
$\text{C.}$ 5
$\text{D.}$ -5
图, 直线 $A B$ 与 $C D$ 相交于点 $\mathrm{O}$, 则 $\angle B O D=$

$\text{A.}$ $40^{\circ}$
$\text{B.}$ $50^{\circ}$
$\text{C.}$ $55^{\circ}$
$\text{D.}$ $60^{\circ}$
计算: $\frac{a^2-5 a}{a-5}=$
$\text{A.}$ $a-5$
$\text{B.}$ $a+5$
$\text{C.}$ 5
$\text{D.}$ $a$
如图 1 是我国古建筑墙上采用的八角形空窗, 其轮廓是一个正八边形, 窗外之境如同镶嵌于一个画框之 中. 如图 2 是八角形空窗的示意图, 它的一个外角 $\angle 1=$

$\text{A.}$ $45^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $110^{\circ}$
$\text{D.}$ $135^{\circ}$
方程 $\frac{2}{x+3}=1$ 的解是
$\text{A.}$ $x=1$
$\text{B.}$ $x=-1$
$\text{C.}$ $x=5$
$\text{D.}$ $x=-5$
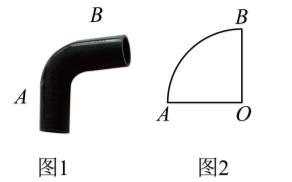
如图 1 是一段弯管, 弯管的部分外轮廓线如图 2 所示是一条圆弧 $\widehat{A B}$, 圆弧的半径 $O A=20 \mathrm{~cm}$, 圆心角 $\angle A O B=90^{\circ}$, 则 $\widehat{A B}=(\quad)$
$\text{A.}$ $20 \pi \mathrm{cm}$
$\text{B.}$ $10 \pi \mathrm{cm}$
$\text{C.}$ $5 \pi \mathrm{cm}$
$\text{D.}$ $2 \pi \mathrm{cm}$
已知二次函数 $y=-3(x-2)^2-3$, 下列说法正确的是
$\text{A.}$ 对称轴为 $x=-2$
$\text{B.}$ 顶点坐标为 $(2,3)$
$\text{C.}$ 函数的最大值是 -3
$\text{D.}$ 函数的最小值是 -3
关于 $\mathrm{x}$ 的一元二次方程 $x^2+b x+c=0$ 有两个相等的实数根, 则 $b^2-2(1+2 c)=(\quad)$
$\text{A.}$ -2
$\text{B.}$ 2
$\text{C.}$ -4
$\text{D.}$ 4
2022 年我国新能源汽车销量持续增长, 全年销量约为 572.6 万辆, 同比增长 $91.7 \%$, 连续 8 年位居全球 第一. 下面的统计图反映了 2021 年、 2022 年新能源汽车月度销量及同比增长速度的情况. (2022 年同比增 长速度 $\left.=\frac{2022 \text { 年当月销量 }-2021 \text { 年当月销量 }}{2021 \text { 年当月销量 }} \times 100 \%\right)$ 根据统计图提供的信息, 下列推断不合理的是

$\text{A.}$ 2021 年新能源汽车月度销量最高是 12 月份, 超过 40 万辆
$\text{B.}$ 2022 年新能源汽车月度销量超过 50 万辆的月份有 6 个
$\text{C.}$ 相对于 2021 年, 2022 年新能源汽车同比增长速度最快的是 2 月份, 达到了 $181.1 \%$
$\text{D.}$ 相对于 2021 年, 2022 年从 5 月份开始新能源汽车同比增长速度持续降低
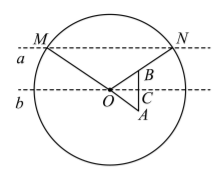
我国古代天文学确定方向的方法中蕴藏了平行线的作图法. 如《淮南子天文训》中记载: “正朝夕: 先 树一表东方; 操一表却去前表十步, 以参望日始出北廉. 日直入, 又树一表于东方, 因西方之表, 以参望 日方入北康. 则定东方两表之中与西方之表, 则东西也. "如图, 用几何语言叙述作图方法: 已知直线 $\mathrm{a}$ 和 直线外一定点 $\mathrm{O}$, 过点 $\mathrm{O}$ 作直线与 $\mathrm{a}$ 平行. (1) 以 $\mathrm{O}$ 为圆心, 单位长为半径作圆, 交直线 $\mathrm{a}$ 于点 $\mathrm{M}, \mathrm{N}$;
(2) 分别在 $M O$ 的延长线及 $O N$ 上取点 $\mathrm{A}, \mathrm{B}$, 使 $O A=O B$; (3) 连接 $A B$, 取其中点 $\mathrm{C}$, 过 $\mathrm{O}, \mathrm{C}$ 两点确 定直线 $\mathrm{b}$, 则直线 $a \| b$. 按以上作图顺序, 若 $\angle M N O=35^{\circ}$, 则 $\angle A O C=(\quad)$
$\text{A.}$ $35^{\circ}$
$\text{B.}$ $30^{\circ}$
$\text{C.}$ $25^{\circ}$
$\text{D.}$ $20^{\circ}$
一次函数 $y=k x-1$ 的函数值 $\mathrm{y}$ 随 $\mathrm{x}$ 的增大而减小, 当 $x=2$ 时, $\mathrm{y}$ 的值可以是
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ -1
$\text{D.}$ -2
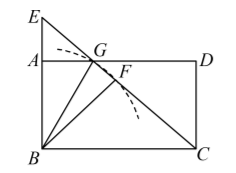
如图, 在矩形 $A B C D$ 中, 点 $\mathrm{E}$ 为 $B A$ 延长线上一点, $\mathrm{F}$ 为 $C E$ 的中点, 以 $\mathrm{B}$ 为圆心, $B F$ 长为半径的圆 弧过 $A D$ 与 $C E$ 的交点 $\mathrm{G}$, 连接 $B G$. 若 $A B=4, C E=10$, 则 $A G=(\quad)$
$\text{A.}$ 2
$\text{B.}$ 2.5
$\text{C.}$ 3
$\text{D.}$ 3.5
填空题 (共 4 题 ),请把答案直接填写在答题纸上
如图, 在 $A B C D$ 中, $B D=C D, A E \perp B D$ 于点 $\mathrm{E}$, 若 $\angle C=70^{\circ}$, 则 $\angle B A E=$

如图, 将面积为 7 的正方形 $O A B C$ 和面积为 9 的正方形 $O D E F$ 分别绕原点 $O$ 顺时针旋转, 使 $O A, O D$ 落在数轴上, 点 $\mathrm{A}, \mathrm{D}$ 在数轴上对应的数字分别为 $\mathrm{a}, \mathrm{b}$, 则 $b-a=$

某学习小组做抛掷一枚瓶盖的实验, 整理的实验数据如下表:

下面有三个推断:
(1)通过上述实验的结果, 可以推断这枚瓶盖有很大的可能性不是质地均匀的;
(2)第 2000 次实验的结果一定是“盖面朝上”;
(3)随着实验次数的增大, “盖面朝上”的概率接近 0.53 .
其中正确的是 . (填序号)
解答题 (共 11 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $\sqrt{3} \times \sqrt{6}-\sqrt{8}$.
解不等式组: $\left\{\begin{array}{c}3 x-1>2(x+1) \\ \frac{x+2}{3}>x-2\end{array}\right.$.
如图, 反比例函数 $y=\frac{k}{x}(x < 0)$ 与一次函数 $y=-2 x+m$ 的图象交于点 $A(-1,4), B C \perp y$ 轴于点 $\mathrm{D}$, 分别交反比例函数与一次函数的图象于点 $\mathrm{B}, \mathrm{C}$.
(1) 求反比例函数 $y=\frac{k}{x}$ 与一次函数 $y=-2 x+m$ 的表达式;
(2) 当 $O D=1$ 时, 求线段 $B C$ 的长.

21. 综合与实践
(1)问题探究:如图 1 是古希腊数学家欧几里得所著的《几何原本》第 1 卷命题 9: “平分一个已知角. ” 即: 作一个已知角的平分线, 如图 2 是欧几里得在 《几何原本》中给出的角平分线作图法: 在 $O A$ 和 $O B$ 上 分别取点 $C$ 和 $\mathrm{D}$, 使得 $O C=O D$, 连接 $C D$, 以 $C D$ 为边作等边三角形 $C D E$, 则 $O E$ 就是 $\angle A O B$ 的平分线.

请写出 $O E$ 平分 $\angle A O B$ 的依据:
(2) 类比迁移: 小明根据以上信息研究发现: $\triangle C D E$ 不一定必须是等边三角形, 只需 $C E=D E$ 即可. 他 查阅资料: 我国古代已经用角尺平分任意角. 做法如下: 如图 3, 在 $\angle A O B$ 的边 $O A, O B$ 上分别取 $O M=O N$, 移动角尺, 使角尺两边相同刻度分别与点 $\mathrm{M}, \mathrm{N}$ 重合, 则过角尺顶点 $\mathrm{C}$ 的射线 $O C$ 是 $\angle A O B$ 的平分线, 请 说明此做法的理由;

(3)拓展实践:
小明将研究应用于实践.如图 4,校园的两条小路 和 ,汇聚形成了一个岔路口 A,现在学校要在两
条小路之间安装一盏路灯 E,使得路灯照亮两条小路(两条小路一样亮),并且路灯 E 到岔路口 A 的距离和
休息椅 D 到岔路口 A 的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示
意图 5 中作出路灯 E 的位置.(保留作图痕迹,不写作法)

如图 1 是我国第一个以“龙”为主题的主题公园——“兰州龙源”. “兰州龙源”的“龙”字主题雕塑以紫铜铸 造, 如巨龙腾空, 气势如虹, 屹立在黄河北岸. 某数学兴趣小组开展了测量“龙”字雕塑 CD 高度的实践活动. 具 体过程如下: 如图 2, “龙”字雕塑 $\mathrm{CD}$ 位于垂直地面的基座 $\mathrm{BC}$ 上, 在平行于水平地面的 $\mathrm{A}$ 处测得 $\angle B A C=38^{\circ}$ 、 $\angle B A D=53^{\circ}, A B=18 \mathrm{~m}$. 求“龙”字雕塑 $C D$ 的高度. ( $\mathrm{B}, \mathrm{C}, \mathrm{D}$ 三点共线, $B D \perp A B$. 结果精确到 $0.1 \mathrm{~m}$ ) (参考数据: $\sin 38^{\circ} \approx 0.62, \cos 38^{\circ} \approx 0.79, \tan 38^{\circ} \approx 0.78, \sin 53^{\circ} \approx 0.80, \cos 53^{\circ} \approx 0.60, \tan 53^{\circ} \approx 1.33$ )

一名运动员在 $10 \mathrm{~m}$ 高的跳台进行跳水, 身体 (看成一点) 在空中的运动轨迹是一条抛物线, 运动员离 水面 $O B$ 的高度 $y(m)$ 与离起跳点 $\mathrm{A}$ 的水平距离 $x(m)$ 之间的函数关系如图所示, 运动员离起跳点 $\mathrm{A}$ 的水平 距离为 $1 m$ 时达到最高点, 当运动员离起跳点 $\mathrm{A}$ 的水平距离为 $3 m$ 时离水面的距离为 $7 m$.
(1) 求 $\mathrm{y}$ 关于 $\mathrm{x}$ 的函数表达式;
(2) 求运动员从起跳点到入水点的水平距离 $O B$ 的长.

如图, 矩形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点 $O, C D \| O E$, 直线 $C E$ 是线段 $O D$ 的垂直平分线, $C E$ 分别交 $O D, A D$ 于点 $\mathrm{F}, \mathrm{G}$, 连接 $D E$.
(1) 判断四边形 $O C D E$ 的形状, 并说明理由;
(2) 当 $C D=4$ 时, 求 $E G$ 的长.

某校八年级共有男生 300 人, 为了解该年级男生排球垫球成绩和掷实心球成绩的情况, 从中随机抽取 40 名男生进行测试, 对数据进行整理、描述和分析, 下面是给出的部分信息.
信息一: 排球垫球成绩如下图所示(成绩用 $\mathrm{x}$ 表示, 分成六组: A. $x < 10$; B. $10 \leq x < 15$; C. $15 \leq x < 20$;
D. $20 \leq x < 25$; E. $25 \leq x < 30$; F. $30 \leq x)$.

(1) 填空: $m=$
(2) 下列结论正确的是 ; (填序号)
①排球垫球成绩超过 10 个的人数占抽取人数的百分比低于 $60 \%$;
② 郑实心球成绩的中位数记为 $\mathrm{n}$, 则 $6.8 \leq n < 7.6$;
③若排球垫球成绩达到 22 个及以上时, 成绩记为优秀. 如果信息四中 6 名男生的两项成绩恰好为优秀的有
如图, $\triangle A B C$ 内接于 $\odot O, A B$ 是 $\odot O$ 的直径, $\overparen{B C}=\widehat{B D}, D E \perp A C$ 于点 $E, D E$ 交 $B F$ 于点 $F$, 交 $A B$ 于点 $G, \angle B O D=2 \angle F$, 连接 $B D$.
(1) 求证: $B F$ 是 $\odot O$ 的切线;
(2) 判断 $\triangle D G B$ 的形状, 并说明理由;
(3) 当 $B D=2$ 时, 求 $F G$ 的长.

在平面直角坐标系中, 给出如下定义: $P$ 为图形 $M$ 上任意一点, 如果点 $P$ 到直线 $E F$ 的距离等于图形 $M$ 上任意两点距离的最大值时, 那么点 $P$ 称为直线 $E F$ 的“伴随点”.
例如: 如图 1, 已知点 $A(1,2), B(3,2), P(2,2)$ 在线段 $A B$ 上, 则点 $P$ 是直线 $E F: x$ 轴的“伴随点”.

(1) 如图 2, 已知点 $A(1,0), B(3,0), P$ 是线段 $A B$ 上一点, 直线 $E F$ 过 $G(-1,0), T\left(0, \frac{\sqrt{3}}{3}\right)$ 两点, 当点 $P$ 是直线 $E F$ 的“伴随点”时, 求点 $P$ 的坐标;
(2) 如图 3, $x$ 轴上方有一等边三角形 $A B C, B C \perp y$ 轴, 顶点 $A$ 在 $y$ 轴上且在 $B C$ 上方, $O C=\sqrt{5}$, 点 $P$ 是 $\triangle A B C$ 上一点, 且点 $P$ 是直线 $E F: x$ 轴的“伴随点”. 当点 $P$ 到 $x$ 轴的距离最小时, 求等边三角形 $A B C$ 的 边长;
(3) 如图 4, 以 $A(1,0), B(2,0), C(2,1)$ 为顶点的正方形 $A B C D$ 上始终存在点 $P$, 使得点 $P$ 是直线 $E F$ : $y=-x+b$ 的“伴随点”. 请直接写出 $b$ 的取值范围.
综合与实践
(1)【思考尝试】
数学活动课上, 老师出示了一个问题: 如图 1, 在矩形 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 是边 $A B$ 上一点, $D F \perp C E$ 于点 $\mathrm{F}, G D \perp D F$, $A G \perp D G, A G=C F$. 试猜想四边形 $A B C D$ 的形状, 并说明理由;
(2)【实践探究】
小䜭受此问题启发, 逆向思考并提出新的问题: 如图 2, 在正方形 $A B C D$ 中, $\mathrm{E}$ 是边 $A B$ 上一点, $D F \perp C E$ 于点 $\mathrm{F}, A H \perp C E$ 于点 $\mathrm{H}, G D \perp D F$ 交 $A H$ 于点 $\mathrm{G}$, 可以用等式表示线段 $F H, A H, C F$ 的数量关系, 请你 思考并解答这个问题;
(3)【拓展迁移】
小博深入研究小㕝提出的这个问题, 发现并提出新的探究点: 如图 3, 在正方形 $A B C D$ 中, $\mathrm{E}$ 是边 $A B$ 上一 点, $A H \perp C E$ 于点 $\mathrm{H}$, 点 $\mathrm{M}$ 在 $C H$ 上, 且 $A H=H M$, 连接 $A M, B H$, 可以用等式表示线段 $C M, B H$ 的数 量关系, 请你思考并解答这个问题.
