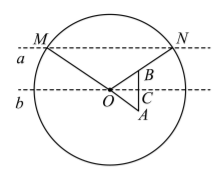
我国古代天文学确定方向的方法中蕴藏了平行线的作图法. 如《淮南子天文训》中记载: “正朝夕: 先 树一表东方; 操一表却去前表十步, 以参望日始出北廉. 日直入, 又树一表于东方, 因西方之表, 以参望 日方入北康. 则定东方两表之中与西方之表, 则东西也. "如图, 用几何语言叙述作图方法: 已知直线 $\mathrm{a}$ 和 直线外一定点 $\mathrm{O}$, 过点 $\mathrm{O}$ 作直线与 $\mathrm{a}$ 平行. (1) 以 $\mathrm{O}$ 为圆心, 单位长为半径作圆, 交直线 $\mathrm{a}$ 于点 $\mathrm{M}, \mathrm{N}$;
(2) 分别在 $M O$ 的延长线及 $O N$ 上取点 $\mathrm{A}, \mathrm{B}$, 使 $O A=O B$; (3) 连接 $A B$, 取其中点 $\mathrm{C}$, 过 $\mathrm{O}, \mathrm{C}$ 两点确 定直线 $\mathrm{b}$, 则直线 $a \| b$. 按以上作图顺序, 若 $\angle M N O=35^{\circ}$, 则 $\angle A O C=(\quad)$