单选题 (共 8 题 ),每题只有一个选项正确
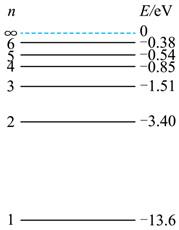
霓虹灯发光原理是不同气体原子从高能级向低能级跃迁时发出能量各异的光子而呈现五 颜六色, 如图为氢原子的能级示意图, 已知可见光光子能量范围为 $1.63 \mathrm{eV} \sim 3.10 \mathrm{eV}$, 若一群 氢原子处于 $n=4$ 能级, 则下列说法正确的是
$\text{A.}$ 这群氢原子自发跃迁时能辐射出 6 种不同频率的可见光
$\text{B.}$ 氢原子从 $n=4$ 能级向 $n=2$ 能级跃迁过程中发出的光为可见光
$\text{C.}$ 辐射出的光中从 $n=2$ 能级跃迁到 $n=1$ 能级发出的光的频率最大
$\text{D.}$ 氢原子从 $n=4$ 能级向 $n=2$ 能级跃迁过程中发出的光去照射逸出功为 $3.2 \mathrm{eV}$ 的金属 䥻, 能使金属钙发生光电效应
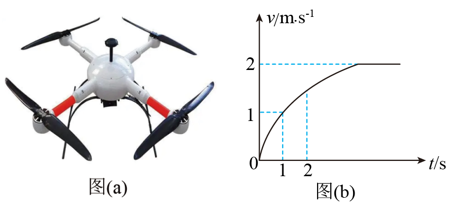
如图(a)所示的无人机具有4个旋翼,可以通过调整旋翼倾斜度而产生不同方向的升力。某次实验,调整旋翼使无人机受竖直向上的恒定升力F从地面静止升起,到达稳定速度过程中,其运动图像如图(b)所示。假设无人机飞行时受到的空气阻力与速率成正比,即 ,方向与速度方向相反,则下列说法正确的是
$\text{A.}$ 无人机在第1 内的位移等于0.5m
$\text{B.}$ 无人机在第 1s内的速度变化量与第2s 内的速度变化量相等
$\text{C.}$ 空气给无人机的作用力逐渐增大
$\text{D.}$ 空气给无人机的作用力逐渐减小
利用智能手机中的磁传感器可以粗测特高压直流输电线中的电流 $I$ 。如图所示, 大致东 西方向水平长直输电导线距地面高度 $20 \mathrm{~m}$, 手机平置于水平长直输电导线正下方, 手机显 示屏所在平面为 $x O y$ 面, $x$ 轴与导线重合, 测量磁感应强度, 然后沿 $y$ 轴方向保持手机平 移前进 $1000 \mathrm{~m}$, 再测量磁感应强度, 数据记录如下表。
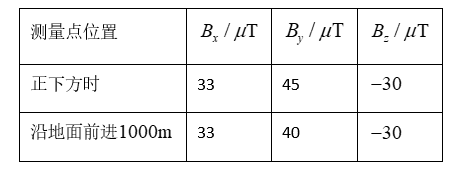
设通有电流 $I$ 的长直导线在距导线 $r$ 处产生磁场的磁感应强度大小为 $B=\frac{k I}{r}$ (其中 $k=2 \times 10^{-7} \mathrm{~T} \cdot \mathrm{m} \cdot \mathrm{A}^{-1}$ ), 该地地磁场为匀强磁场, 前进 $1000 \mathrm{~m}$ 后电流影响可忽略。忽略 其他影响, 根据实验数据, 判断下列说法正确的是
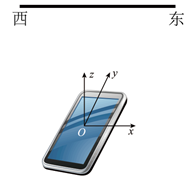
$\text{A.}$ 地磁场方向为沿 $y$ 轴方向
$\text{B.}$ 地磁场的磁感应强度为 $40 \mu \mathrm{T}$
$\text{C.}$ 长导线中电流方向为东向西
$\text{D.}$ 输电线中电流的大小约为 $500 \mathrm{~A}$
2023 年 2 月 26 日和 27 日, 景德镇二中和景德镇二中分别举行了 2023 届成人礼暨高考百 日冲刺誓师大会 (如图)。如图 1 为大会上某队列的走方阵示意图, $A B$ 与 $C D$ 垂直操场跑 道, 某时刻该队伍前排刚到直线 $A B$ 处, 正在 $D$ 点的政教处工作人员准备沿直线 $D C$ 方向 从静止开始穿到对面, 已知工作人员的速度 $v_1$ 的平方 $v_1^2$ 与人离 $D$ 点的距离 $x$ 变化的关系如 图 2 所示, $A B$ 与 $C D$ 相距 $6 \mathrm{~m}$, 队列前进的速度 $v_2$ 为 $1 \mathrm{~m} / \mathrm{s}$, 操场宽 $12 \mathrm{~m}$, 则以下说法正 确的是

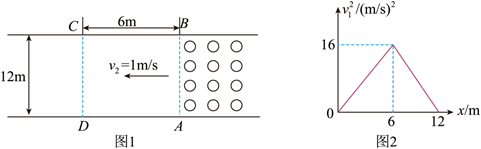
$\text{A.}$ 该工作人员会在到达 $C$ 点之前影响到队伍前进
$\text{B.}$ 该工作人员穿过操场用时 $4 \mathrm{~s}$
$\text{C.}$ 该工作人员的加速度大小为 $\frac{5}{3} \mathrm{~m} / \mathrm{s}^2$
$\text{D.}$ 该工作人员相对队伍最大的速度为 $\sqrt{17} \mathrm{~m} / \mathrm{s}$
如图所示, 两个半径均为 $R$ 的光滑圆轨道 $a 、 b$ 并排固定在坚直平面内, 在轨道最低点 放置一根质量为 $m$ 的铜棒, 棒长为 $L$, 所在空间有平行于圆轨道平面水平向右的匀强磁 场, 给铜榛通以从 $C$ 到 $D$ 的恒定电流 $I$ 的同时给铜棒二大小为 $\sqrt{g R}$ 的水平初速度, 已知 磁感应强度大小 $B=\frac{2 m g}{I L}$ ( $g$ 为重力加速度), 以下说法正确的是
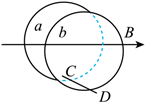
$\text{A.}$ 铜棒获得初速度时对每条轨道的压力为 $m g$
$\text{B.}$ 铜棒获得初速度时对每条轨道的压力为 0
$\text{C.}$ 从轨道最低点到最高点的过程中, 铜棒机械能增加 $2 m g R$
$\text{D.}$ 从轨道最低点到最高点的过程中, 铜棒所受合力做功为 0
用质量为 $m$ 的小铁锤以速度 $v_1$ 向下击打一块质量为 $M$ 的砖块 (击打时间极短), 击打
后, 小铁锤以 $\frac{1}{2} v_1$ 的速率反向弹回, 已知砖块受到击打后在手中的缓冲时间为 $t$, 重力加速 度为 $g$, 下列说法正确的是
$\text{A.}$ 在击打过程中, 铁锤所受合外力的冲量大小为 $\frac{1}{2} m v_1$
$\text{B.}$ 在击打过程中, 铁锤重力的冲量大小为 $m g t$
$\text{C.}$ 砖头缓冲过程中, 对手的压力大小为 $M g$
$\text{D.}$ 砖头缓冲过程中, 对手的压力大小为 $M g+\frac{3 m v_1}{2 t}$
2023年春节,改编自刘慈欣科幻小说的《流浪地球2》电影在全国上映。电影中的太空电梯场景非常震撼。太空电梯的原理并不复杂,与生活的中的普通电梯十分相似。只需在地球同步轨道上建造一个空间站,并用某种足够长也足够结实的“绳索”将其与地面相连,当空间站围绕地球运转时,绳索会细紧,宇航员、乘客以及货物可以通过电梯轿厢一样的升降舱沿绳索直入太空,这样不需要依靠火箭、飞船这类复杂航天工具。如乙图所示,假设有一长度为 的太空电梯连接地球赤道上的固定基地与同步空间站 ,相对地球静止,卫星 与同步空间站 的运行方向相同,此时二者距离最近,经过时间 之后, 第一次相距最远。已知地球半径 ,自转周期 ,下列说法正确的是

$\text{A.}$ 太空电梯各点均处于完全失重状态
$\text{B.}$ $b$ 卫星的周期为 $T_b=\frac{2 T t}{2 t-T}$
$\text{C.}$ 太空电梯停在距地球表面高度为 $2 R$ 的站点, 该站点处的重力加速度
$$
g=\frac{4 \pi^2}{T^2}\left[\frac{(r+R)^3}{9 R^2}-3 R\right]
$$
$\text{D.}$ 太空电梯上各点线速度与该点离地球球心距离成反比
如图甲所示, 直径为 $D$ 、深度为 $H$ 的圆柱形容器内充满某种透明液体, 在其底部正中央 放置二点光源 $S$, 从液面上方看, 直径为 $d$ 的液面被光源照亮, 某物理兴趣小组想要让光 源能够照亮容器的整个液面, 在容器底部中央镶嵌二直径为 $L$ 的圆形平面镜 $M N$ (上表面 与容器底上表面齐平), 并把光源向上移动一段距离 $h$, 如图乙所示, 则
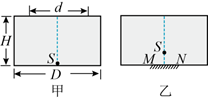
$\text{A.}$ 该液体的折射率 $n=\frac{\sqrt{d^2+4 H^2}}{d}$
$\text{B.}$ 该液体的折射率 $n=\frac{\sqrt{d^2+4 H^2}}{2 H}$
$\text{C.}$ 平面镜的直径 $L \geq D-d$
$\text{D.}$ 光源上移的距离 $h \geq \frac{H(D-d)}{d}$
多选题 (共 2 题 ),每题有多个选项正确
如图所示, 质量均为 $m$ 的物块 $\mathrm{A} 、 \mathrm{~B}$ 用轻弹簧连接并坚直放置, 轻绳绕过分别固定在同 一水平面上 $O 、 E$ 两点的定滑轮一端与物块 $\mathrm{A}$ 相连, 另一端与质量为 $m$ 的小球 $\mathrm{C}$ 相连, 小 球 $\mathrm{C}$ 套在水平固定、粗细均匀的光滑直杆上。开始时, 小球 $\mathrm{C}$ 锁定在直杆的 $P$ 点, 连接小 球的轻绳与水平方向的夹角为 $\theta=53^{\circ}$, 物块 $\mathrm{B}$ 对地面的压力恰好为零。某时刻解除对小 球 $\mathrm{C}$ 的锁定, 同时对小球 $\mathrm{C}$ 施加一个水平向右、大小为 $F$ 的恒力, 小球 $\mathrm{C}$ 运动到直杆 $Q$ 点时的速度达到最大, $O Q$ 与水平方向的夹角也为 $\theta, D$ 点为 $P 、 Q$ 两点的中点, $P 、 Q$ 两点间的距离为 $L, E$ 点在物块 $\mathrm{A}$ 的正上方, 小球 $\mathrm{C}$ 运动过程中轻绳始终处于拉直状态, 弹簧始终在弹性限度内。忽略两定滑轮的大小, 已知重力加速度大小为 $g$, $\sin 53^{\circ}=\frac{4}{5}, \cos 53^{\circ}=\frac{3}{5}$ 。下列说法正确的是

$\text{A.}$ 小球 $\mathrm{C}$ 从 $P$ 点运动到 $D$ 点的过程中, 合外力对物块 $\mathrm{A}$ 做的功不为零
$\text{B.}$ 小球 $\mathrm{C}$ 从 $P$ 点运动到 $D$ 点的过程中, 弹簧的弹力和轻绳的拉力以及物块 $\mathrm{A}$ 的重力对物 块 $\mathrm{A}$ 冲量的和为零
$\text{C.}$ 小球 $\mathrm{C}$ 运动到 $Q$ 点时的速度大小为 $\sqrt{\frac{25 F L}{17 m}}$
$\text{D.}$ 小球 $\mathrm{C}$ 运动到 $Q$ 点时物块 $\mathrm{A}$ 的加速度大小为 $\left|\frac{5 F}{4 m}-2 g\right|$
如图, 光滑绝缘水平面上, 由 $1 、 2 、 3$ 三个带电量均为 $+q$ 、质量均为 $m$ 的相同金属小球, 用长均为 $L$ 的三根轻质绝缘细绳连接, $A 、 B 、 C$ 分别为其中点, $O$ 为三角形中心, 已知单个 点电荷 $q$ 周围空间的电势 $\varphi=k \frac{q}{r}, r$ 为到点电荷的距离, 则下列说法正确的是
$\text{A.}$ $O$ 点的电场强度为零
$\text{B.}$ 长度 $L$ 取合适值时, $A 、 O$ 两点的电势可能相等
$\text{C.}$ 系统的总电势能为 $E_{\mathrm{p}}=k \frac{3 q^2}{L}$
$\text{D.}$ 若 $B$ 处剪断, 则之后小球 1 的最大速度为 $v_{1 \mathrm{~m}}=q \sqrt{\frac{2 k}{3 m L}}$
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某班王同学所用水杯的容积 $V=480 \mathrm{~mL}$, 如图所示, 盖上杯盖可以把一定量的空气密封 在杯内, 上午第一节课间向保温杯中注入水温为 $87^{\circ} \mathrm{C}$ 的饮用水 $240 \mathrm{~mL}$, 盖上杯盖到第二节 课间时水温变成 $47^{\circ} \mathrm{C}$, 打开杯盖喝掉一半水, 再盖上杯盖, 设封入水杯内的空气的温度很 快跟杯内饮用水的温度相同, 忽略水蒸气对空气体积的影响和热水因温度变化而引起的体
积变化, 热力学温度与摄氏温度的关系 $T=273+t$, 大气压强为 $p_0=1.0 \times 10^5 \mathrm{~Pa}$, 求:
(1) 第二节课间打开杯盖前杯内空气的压强 $p$ (保留两位有效数字);
(2) 两次盖上杯盖保温杯内封人空气的质量之比。

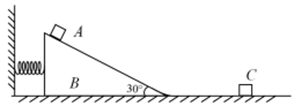
用一根轻弹簧坚直悬挂一物块 $\mathrm{A}$, 静止时弹簧伸长了 $x$ 。现将该弹簧左端固定在墙 上, 右端与 二直角三棱体 $\mathrm{B}$ 的侧面接触 (不粘连), 先将弹簧压缩 $\frac{\sqrt{3}}{8} x$, 然后让物热 $\mathrm{A}$ 从 离地面高度为 $x$ 处由静止释放, 发现 $\mathrm{A}$ 沿斜面下滑时 $\mathrm{B}$ 刚好保持静止。若 $\mathrm{A}$ 离开斜面滑到水平地面时无能量损失, 当 $\mathrm{B}$ 速度最大时, $\mathrm{A}$ 恰好与水平面上的小物块 $\mathrm{C}$ 发生弹性碰撞, 碰后 $\mathrm{A}$ 和 $\mathrm{B}$ 距离不变。已知水平地面光滑, 斜面倾角为 $30^{\circ}, \mathrm{A}$ 和 $\mathrm{B}$ 的质量相等, 已知弹 簧振子的振动周期公式为 $T=2 \pi \sqrt{\frac{m}{k}}$ 弹簧弹性势能 $E_{\mathrm{p}}$ 与形变量 $\Delta \mathrm{x}$ 的关系为 $E_{\mathrm{p}}=\frac{1}{2} k(\Delta x)^2$, 重力加速度为 $g$ 。求:
(1) 物块 $\mathrm{A}$ 在斜面上下滑时的加速度大小和物热 $\mathrm{A}$ 与斜面之间的动摩擦因数;
(2) 碰后 $\mathrm{A}$ 与 $\mathrm{B}$ 斜面底端的距离;
(3) $\mathrm{A}$ 和 $\mathrm{C}$ 的质量比。
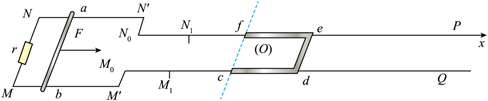
如图所示, 有形状为 “工”” 的光滑平行导轨 $M Q$ 和 $N P$ 水平放置, 其中宽轨间距为 $2 d$, 窄轨间距为 $d$, 轨道足够长。 $N_1 M_1$ 右侧均为绝缘材料, 其余为金属导轨, $N_0 N_1=M_0 M_1=d$ 。 $M N$ 间接有一电阻阻值为 $r$ 。金属棒 $a b$ 质量为 $m$ 、长度为 $2 d$ 、电阻阻值为 $2 r$, 在水平向右、 大小为 $F$ 的恒力作用下, 从静止开始加速, 离开宽轨前, 速度已达最大值。金属棒滑上窄轨 瞬间, 迅速撤去力 $F$ 。 $c$ def 是质量为 $m$ 、电阻阻值为 $r$ 、三边长度均为 $d$ 的 “ $\mathrm{U}$ ” 形金属框, 如图平放在绝缘导轨上。以 $f$ 点所在处为坐标原点 $O$, 沿 $f e P$ 方向建立坐标轴 $O x$ 。整个空 间存在竖直向上的磁场, $c f$ 左侧为磁感应强度为 $\mathrm{B}_0$ 的匀强磁场, $c f$ 右侧磁感应强度分布 规律 $B=B_0+k x(x . .0)$, 其中 $k>0$, 金属导轨电阻不计, $a b$ 棒、金属框与导轨始终接 触良好。
(1) 求 $a b$ 棒在宽轨上运动的最大速度 $v_{\mathrm{m}}$ 及刚滑上窄轨时 $a b$ 两端电压 $U_{a b}$;
(2) 求 $a b$ 棒运动至与金属框碰撞前瞬间的速度大小 $v_1$;
(3) 若 $a b$ 棒与金属框碰撞后连接在一起, 求金属框静止时 $f$ 端的位置坐标 $x$ 。