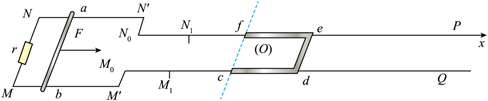
如图所示, 有形状为 “工”” 的光滑平行导轨 $M Q$ 和 $N P$ 水平放置, 其中宽轨间距为 $2 d$, 窄轨间距为 $d$, 轨道足够长。 $N_1 M_1$ 右侧均为绝缘材料, 其余为金属导轨, $N_0 N_1=M_0 M_1=d$ 。 $M N$ 间接有一电阻阻值为 $r$ 。金属棒 $a b$ 质量为 $m$ 、长度为 $2 d$ 、电阻阻值为 $2 r$, 在水平向右、 大小为 $F$ 的恒力作用下, 从静止开始加速, 离开宽轨前, 速度已达最大值。金属棒滑上窄轨 瞬间, 迅速撤去力 $F$ 。 $c$ def 是质量为 $m$ 、电阻阻值为 $r$ 、三边长度均为 $d$ 的 “ $\mathrm{U}$ ” 形金属框, 如图平放在绝缘导轨上。以 $f$ 点所在处为坐标原点 $O$, 沿 $f e P$ 方向建立坐标轴 $O x$ 。整个空 间存在竖直向上的磁场, $c f$ 左侧为磁感应强度为 $\mathrm{B}_0$ 的匀强磁场, $c f$ 右侧磁感应强度分布 规律 $B=B_0+k x(x . .0)$, 其中 $k>0$, 金属导轨电阻不计, $a b$ 棒、金属框与导轨始终接 触良好。
(1) 求 $a b$ 棒在宽轨上运动的最大速度 $v_{\mathrm{m}}$ 及刚滑上窄轨时 $a b$ 两端电压 $U_{a b}$;
(2) 求 $a b$ 棒运动至与金属框碰撞前瞬间的速度大小 $v_1$;
(3) 若 $a b$ 棒与金属框碰撞后连接在一起, 求金属框静止时 $f$ 端的位置坐标 $x$ 。
(1) 求 $a b$ 棒在宽轨上运动的最大速度 $v_{\mathrm{m}}$ 及刚滑上窄轨时 $a b$ 两端电压 $U_{a b}$;
(2) 求 $a b$ 棒运动至与金属框碰撞前瞬间的速度大小 $v_1$;
(3) 若 $a b$ 棒与金属框碰撞后连接在一起, 求金属框静止时 $f$ 端的位置坐标 $x$ 。
