如图甲所示, 直径为 $D$ 、深度为 $H$ 的圆柱形容器内充满某种透明液体, 在其底部正中央 放置二点光源 $S$, 从液面上方看, 直径为 $d$ 的液面被光源照亮, 某物理兴趣小组想要让光 源能够照亮容器的整个液面, 在容器底部中央镶嵌二直径为 $L$ 的圆形平面镜 $M N$ (上表面 与容器底上表面齐平), 并把光源向上移动一段距离 $h$, 如图乙所示, 则
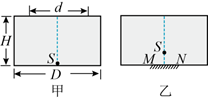

A. 该液体的折射率 $n=\frac{\sqrt{d^2+4 H^2}}{d}$
B. 该液体的折射率 $n=\frac{\sqrt{d^2+4 H^2}}{2 H}$
C. 平面镜的直径 $L \geq D-d$
D. 光源上移的距离 $h \geq \frac{H(D-d)}{d}$