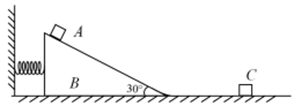
用一根轻弹簧坚直悬挂一物块 $\mathrm{A}$, 静止时弹簧伸长了 $x$ 。现将该弹簧左端固定在墙 上, 右端与 二直角三棱体 $\mathrm{B}$ 的侧面接触 (不粘连), 先将弹簧压缩 $\frac{\sqrt{3}}{8} x$, 然后让物热 $\mathrm{A}$ 从 离地面高度为 $x$ 处由静止释放, 发现 $\mathrm{A}$ 沿斜面下滑时 $\mathrm{B}$ 刚好保持静止。若 $\mathrm{A}$ 离开斜面滑到水平地面时无能量损失, 当 $\mathrm{B}$ 速度最大时, $\mathrm{A}$ 恰好与水平面上的小物块 $\mathrm{C}$ 发生弹性碰撞, 碰后 $\mathrm{A}$ 和 $\mathrm{B}$ 距离不变。已知水平地面光滑, 斜面倾角为 $30^{\circ}, \mathrm{A}$ 和 $\mathrm{B}$ 的质量相等, 已知弹 簧振子的振动周期公式为 $T=2 \pi \sqrt{\frac{m}{k}}$ 弹簧弹性势能 $E_{\mathrm{p}}$ 与形变量 $\Delta \mathrm{x}$ 的关系为 $E_{\mathrm{p}}=\frac{1}{2} k(\Delta x)^2$, 重力加速度为 $g$ 。求:
(1) 物块 $\mathrm{A}$ 在斜面上下滑时的加速度大小和物热 $\mathrm{A}$ 与斜面之间的动摩擦因数;
(2) 碰后 $\mathrm{A}$ 与 $\mathrm{B}$ 斜面底端的距离;
(3) $\mathrm{A}$ 和 $\mathrm{C}$ 的质量比。
(1) 物块 $\mathrm{A}$ 在斜面上下滑时的加速度大小和物热 $\mathrm{A}$ 与斜面之间的动摩擦因数;
(2) 碰后 $\mathrm{A}$ 与 $\mathrm{B}$ 斜面底端的距离;
(3) $\mathrm{A}$ 和 $\mathrm{C}$ 的质量比。
