单选题 （共 10 题 ），每题只有一个选项正确
2 的相反数是
$\text{A.}$ 2
$\text{B.}$ -2
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $-\frac{1}{2}$
我国自主研发的 $500 \mathrm{~m}$ 口径球面射电望远镜 (FAST) 有 “中国天眼”之称, 它的反射面面积约为 $2500000 \mathrm{~m}^2$. 用科学记数法表示数据 250000 为
$\text{A.}$ $0.25 \times 10^6$
$\text{B.}$ $25 \times 10^4$
$\text{C.}$ $2.5 \times 10^4$
$\text{D.}$ $2.5 \times 10^5$
下列计算结果正确的是
$\text{A.}$ $a^8 \div a^2=a^4$
$\text{B.}$ $5 a b-2 a b=3$
$\text{C.}$ $(a-b)^2=a^2-b^2$
$\text{D.}$ $\left(-a b^3\right)^2=a^2 b^6$
不等式 $x \geq 1$ 的解集在数轴上表示正确的是
$\text{A.}$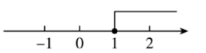 
$\text{B.}$ 
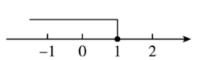$\text{C.}$ 
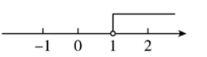$\text{D.}$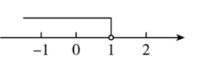 
某班级准备利用暑假去研学旅行, 他们准备定做一批容量一致的双肩包·为此, 活动负责人征求了班内同 学的意向, 得到了如下数据:
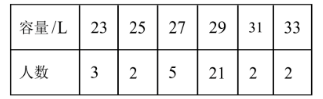
则双肩包容量的众数是
$\text{A.}$ $21 \mathrm{~L}$
$\text{B.}$ $23 \mathrm{~L}$
$\text{C.}$ $29 \mathrm{~L}$
$\text{D.}$ $33 \mathrm{~L}$
下列说法正确的是
$\text{A.}$ 将油滴入水中, 油会浮在水面上是不可能事件
$\text{B.}$ 抛出的篮球会下落是随机事件
$\text{C.}$ 了解一批圆珠笔芯的使用寿命, 采用普查的方式
$\text{D.}$ 若甲、乙两组数据的平均数相同, $S_{\text {甲 }}^2=2, S_{\mathrm{Z}}^2=2.5$, 则甲组数据较稳定
已知一次函数 $y=k x+b$ 的图象如图所示, 则 $k, b$ 的取值范围是
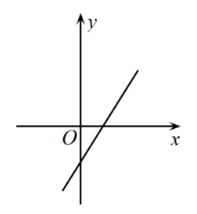
$\text{A.}$ $k>0, b < 0$
$\text{B.}$ $k < 0, b < 0$
$\text{C.}$ $k < 0, b>0$
$\text{D.}$ $k>0, b>0$
二次函数 $y=-(x+1)^2+2$ 图象的顶点所在的象限是
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
如图, 四边形 $A B C D$ 内接于 $\square O, \square O$ 的半径为 $3, \angle D=120^{\circ}$, 则弧$A C$ 的长是
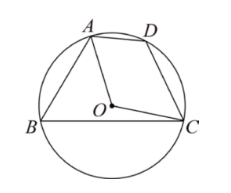
$\text{A.}$ $\pi$
$\text{B.}$ $\frac{2}{3} \pi$
$\text{C.}$ $2 \pi$
$\text{D.}$ $4 \pi$
填空题 （共 6 题 ），请把答案直接填写在答题纸上
当 $a+b=3$ 时, 代数式 $2(a+2 b)-(3 a+5 b)+5$ 的值为
若点 $A\left(-2, y_1\right)$ 和点 $B\left(-1, y_2\right)$ 都在反比例函数 $y=\frac{2}{x}$ 的图象上, 则 $y_1$ $y_2$.
如图, 直线 $A B / / C D$, 直线 $E F$ 分别与 $A B, C D$ 交于点 $E, F$, 小明同学利用尺规按以下步骤作 图:
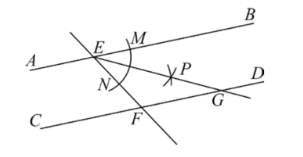
(1) 点 $E$ 为圆心, 以任意长为半径作弧交射线 $E B$ 于点 $M$, 交射线 $E F$ 于点 $N$;
(2) 分别以点 $M, N$ 为圆心, 以大于 $\frac{1}{2} M N$ 的长为半径作弧, 两弧在 $\angle B E F$ 内交于点 $P$;
(3) 作射线 $E P$ 交直线 $C D$ 于点 $G$; 若 $\angle E G F=29^{\circ}$, 则 $\angle B E F=$ 度.
如图, 王叔叔想用长为 $60 \mathrm{~m}$ 的栅栏, 再借助房屋的外墙围成一个矩形羊圈 $A B C D$, 已知房屋外墙足够 长, 当矩形 $A B C D$ 的边 $A B=$ ________ $\mathrm{m}$ 时, 羊圈的面积最大.
如图, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A C=B C=3$, 点 $D$ 在直线 $A C$ 上, $A D=1$, 过点 $D$ 作 $D E / / A B$ 直线 $B C$ 于点 $E$, 连接 $B D$, 点 $O$ 是线段 $B D$ 的中点, 连接 $O E$, 则 $O E$ 的长为
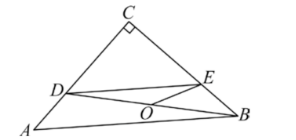
解答题 （共 9 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(\pi-2023)^0+\sqrt{(-2)^2}+\left(\frac{1}{3}\right)^{-2}-4 \sin 30^{\circ}$.
为弘扬中华优秀传统文化, 学校举办“经典诵读”比赛, 将比赛内容分为“唐诗”“宋词”“元曲”三类 (分别 用 A, $B, C$ 依次表示这三类比赛内容). 现将正面写有 $\mathrm{A}, B, C$ 的三张完全相同的卡片背面朝上洗匀, 由选手抽取卡片确定比赛内容. 选手小明先从三张卡片中随机抽取一张, 记下字母后放回洗匀, 选手小梅再 随机抽取一张, 记下字母·请用画树状图或列表的方法, 求小明和小梅抽到同一类比赛内容的概率.
如图, 在 $\triangle A B C$ 中, $A B=A C, A D$ 是 $B C$ 边上的中线, 点 $E$ 在 $D A$ 的延长线上, 连接 $B E$, 过点 $C$ 作 $C F / / B E$ 交 $A D$ 的延长线于点 $F$, 连接 $B F 、 C E$, 求证: 四边形 $B E C F$ 是菱形.
书香润沈城, 阅读向末来”, 沈阳市第十五届全民读书季启动之际. 某中学准备购进一批图书供学生 阅读, 为了合理配备各类图书, 从全体学生中随机抽取了部分学生进行了问卷调查 - 问卷设置了五种选项: $A$ “艺术类”, $B$ “文学类”, $C$ “科普类”, $D$ “体育类”, $E$ “其他类”, 每名学生必须且只能选择 其中最喜爱的一类图书, 将调查结果整理绘制成如下两幅不完整的统计图.
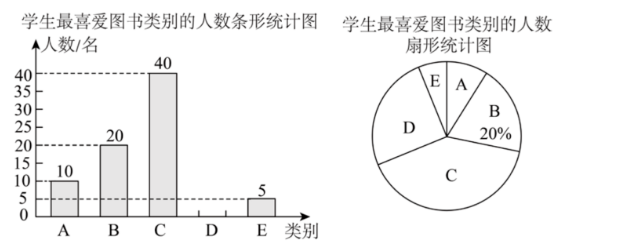
根据以上信息, 解答下列问题:
(1) 此次被调查的学生人数为 ________ 名;
(2) 请直接补全条形统计图;
(3) 在扇形统计图中, A “艺术类” 所对应的圆心角度数是 ________ 度；
(4) 据抽样调查结果, 请你估计该校 1800 名学生中, 有多少名学生最喜爱 $C$ “科普类” 图书.
甲、乙两人加工同一种零件, 每小时甲比乙多加工 2 个这种零件, 甲加工 25 个这种零件所用的时间与 乙加工 20 个这种零件所用的时间相等, 求乙每小时加工多少个这种零件.
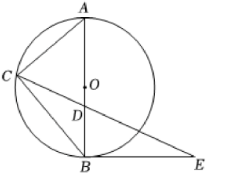
如图, $A B$ 是 $\odot O$ 的直径, 点 $C$ 是 $ \odot O$ 上的一点 (点 $C$ 不与点 $\mathrm{A}, B$ 重合), 连接 $A C 、 B C$, 点 $D$ 是 $A B$ 上的一点, $A C=A D, B E$ 交 $C D$ 的延长线于点 $E$, 且 $B E=B C$.
(1) 求证: $B E$ 是 $\odot O$ 的切线;
(2) 若 $\odot O$ 的半径为 $5, \tan E=\frac{1}{2}$, 则 $B E$ 的长为
如图, 在平面直角坐标系中, 一次函数 $y=k x+b$ 的图象交 $x$ 轴于点 $A(8,0)$, 交 $y$ 轴于点 $B$. 直线 $y=\frac{1}{2} x-\frac{3}{2}$ 与 $y$ 轴交于点 $D$, 与直线 $A B$ 交于点 $C(6, a)$. 点 $M$ 是线段 $B C$ 上的一个动点 (点 $M$ 不与点 $C$ 重合), 过点 $M$ 作 $x$ 轴的垂线交直线 $C D$ 于点 $N$. 设点 $M$ 的横坐标为 $m$.
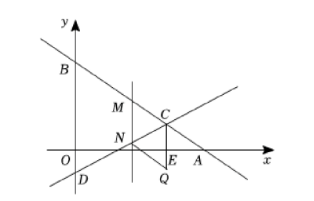
(1) 求 $a$ 的值和直线 $A B$ 的函数表达式;
(2) 以线段 $M N, M C$ 为邻边作 $\square M N Q C$, 直线 $Q C$ 与 $x$ 轴交于点 $E$.
①当 $0 \leq m < \frac{24}{5}$ 时, 设线段 $E Q$ 的长度为 $l$, 求 $l$ 与 $m$ 之间的关系式;
②连接 $O Q, A Q$, 当 $\triangle A O Q$ 的面积为 3 时, 请直接写出 $m$ 的值.
如图1, 在 $\square A B C D$ 纸片中, $A B=10, A D=6, \angle D A B=60^{\circ}$, 点 $E$ 为 $B C$ 边上的一点 (点 $E$ 不与 点 $C$ 重合), 连接 $A E$, 将 $\square A B C D$ 纸片沿 $A E$ 所在直线折叠, 点 $C, D$ 的对应点分别为 $C^{\prime} 、 D^{\prime}$, 射线 $C^{\prime} E$ 与射线 $A D$ 交于点 $F$.
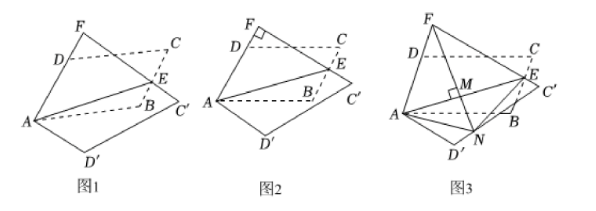
(1) 求证: $A F=E F$;
(2) 如图 2, 当 $E F \perp A F$ 时, $D F$ 的长为
(3) 如图 3, 当 $C E=2$ 时, 过点 $F$ 作 $F M \perp A E$, 垂足为点 $M$, 延长 $F M$ 交 $C^{\prime} D^{\prime}$ 于点 $N$, 连接 $A N 、 E N$, 求 $\triangle A N E$ 的面积.
如图, 在平面直角坐标系中, 二次函数 $y=\frac{1}{3} x^2+b x+c$ 的图象经过点 $A(0,2)$, 与 $x$ 轴的交点为点 $B(\sqrt{3}, 0)$ 和点 $C$.
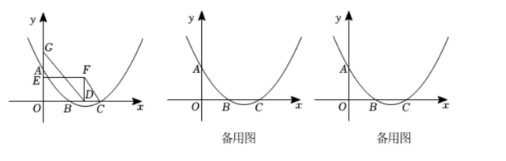
（1）求这个二次函数的表达式;
(2) 点 $E, G$ 在 $y$ 轴正半轴上, $O G=2 O E$, 点 $D$ 在线段 $O C$ 上, $O D=\sqrt{3} O E$. 以线段 $O D, O E$ 为邻 边作矩形 $O D F E$, 连接 $G D$, 设 $O E=a$.
①连接 $F C$, 当 $\triangle G O D$ 与 $\triangle F D C$ 相似时, 求 $a$ 的值;
②当点 $D$ 与点 $C$ 重合时, 将线段 $G D$ 绕点 $G$ 按逆时针方向旋转 $60^{\circ}$ 后得到线段 $G H$, 连接 $F H, F G$, 将 $\square G F H$ 绕点 $F$ 按顺时针方向旋转 $\alpha\left(0^{\circ} < \alpha \leq 180^{\circ}\right)$ 后得到 $\triangle G^{\prime} F H^{\prime}$, 点 $G, H$ 的对应点分别为 $G^{\prime} 、 H^{\prime}$, 连接 $D E$. 当 $\Delta G^{\prime} F H^{\prime}$ 的边与线段 $D E$ 垂直时, 请直接写出点 $H^{\prime}$ 的横坐标.