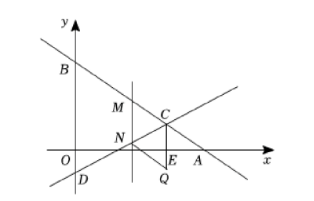
如图, 在平面直角坐标系中, 一次函数 $y=k x+b$ 的图象交 $x$ 轴于点 $A(8,0)$, 交 $y$ 轴于点 $B$. 直线 $y=\frac{1}{2} x-\frac{3}{2}$ 与 $y$ 轴交于点 $D$, 与直线 $A B$ 交于点 $C(6, a)$. 点 $M$ 是线段 $B C$ 上的一个动点 (点 $M$ 不与点 $C$ 重合), 过点 $M$ 作 $x$ 轴的垂线交直线 $C D$ 于点 $N$. 设点 $M$ 的横坐标为 $m$.
(1) 求 $a$ 的值和直线 $A B$ 的函数表达式;
(2) 以线段 $M N, M C$ 为邻边作 $\square M N Q C$, 直线 $Q C$ 与 $x$ 轴交于点 $E$.
①当 $0 \leq m < \frac{24}{5}$ 时, 设线段 $E Q$ 的长度为 $l$, 求 $l$ 与 $m$ 之间的关系式;
②连接 $O Q, A Q$, 当 $\triangle A O Q$ 的面积为 3 时, 请直接写出 $m$ 的值.

(1) 求 $a$ 的值和直线 $A B$ 的函数表达式;
(2) 以线段 $M N, M C$ 为邻边作 $\square M N Q C$, 直线 $Q C$ 与 $x$ 轴交于点 $E$.
①当 $0 \leq m < \frac{24}{5}$ 时, 设线段 $E Q$ 的长度为 $l$, 求 $l$ 与 $m$ 之间的关系式;
②连接 $O Q, A Q$, 当 $\triangle A O Q$ 的面积为 3 时, 请直接写出 $m$ 的值.