如图1, 在
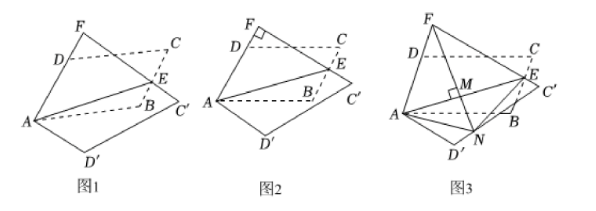
(1) 求证:
(2) 如图 2, 当
(3) 如图 3, 当

(1) 求证:
(2) 如图 2, 当
(3) 如图 3, 当