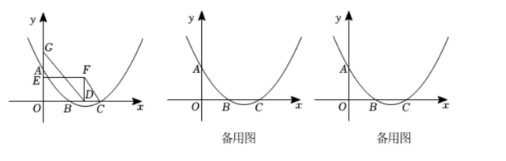
如图, 在平面直角坐标系中, 二次函数 $y=\frac{1}{3} x^2+b x+c$ 的图象经过点 $A(0,2)$, 与 $x$ 轴的交点为点 $B(\sqrt{3}, 0)$ 和点 $C$.
(1)求这个二次函数的表达式;
(2) 点 $E, G$ 在 $y$ 轴正半轴上, $O G=2 O E$, 点 $D$ 在线段 $O C$ 上, $O D=\sqrt{3} O E$. 以线段 $O D, O E$ 为邻 边作矩形 $O D F E$, 连接 $G D$, 设 $O E=a$.
①连接 $F C$, 当 $\triangle G O D$ 与 $\triangle F D C$ 相似时, 求 $a$ 的值;
②当点 $D$ 与点 $C$ 重合时, 将线段 $G D$ 绕点 $G$ 按逆时针方向旋转 $60^{\circ}$ 后得到线段 $G H$, 连接 $F H, F G$, 将 $\square G F H$ 绕点 $F$ 按顺时针方向旋转 $\alpha\left(0^{\circ} < \alpha \leq 180^{\circ}\right)$ 后得到 $\triangle G^{\prime} F H^{\prime}$, 点 $G, H$ 的对应点分别为 $G^{\prime} 、 H^{\prime}$, 连接 $D E$. 当 $\Delta G^{\prime} F H^{\prime}$ 的边与线段 $D E$ 垂直时, 请直接写出点 $H^{\prime}$ 的横坐标.

(1)求这个二次函数的表达式;
(2) 点 $E, G$ 在 $y$ 轴正半轴上, $O G=2 O E$, 点 $D$ 在线段 $O C$ 上, $O D=\sqrt{3} O E$. 以线段 $O D, O E$ 为邻 边作矩形 $O D F E$, 连接 $G D$, 设 $O E=a$.
①连接 $F C$, 当 $\triangle G O D$ 与 $\triangle F D C$ 相似时, 求 $a$ 的值;
②当点 $D$ 与点 $C$ 重合时, 将线段 $G D$ 绕点 $G$ 按逆时针方向旋转 $60^{\circ}$ 后得到线段 $G H$, 连接 $F H, F G$, 将 $\square G F H$ 绕点 $F$ 按顺时针方向旋转 $\alpha\left(0^{\circ} < \alpha \leq 180^{\circ}\right)$ 后得到 $\triangle G^{\prime} F H^{\prime}$, 点 $G, H$ 的对应点分别为 $G^{\prime} 、 H^{\prime}$, 连接 $D E$. 当 $\Delta G^{\prime} F H^{\prime}$ 的边与线段 $D E$ 垂直时, 请直接写出点 $H^{\prime}$ 的横坐标.