单选题 （共 7 题 ），每题只有一个选项正确
2022年10月，我国自主研发的“夸父一号”太阳探测卫星成功发射。该卫星搭载的莱曼阿尔法太阳望远镜可用于探测波长为 的氢原子谱线（对应的光子能量为 ）。根据如图所示的氢原子能级图，可知此谱线来源于太阳中氢原子
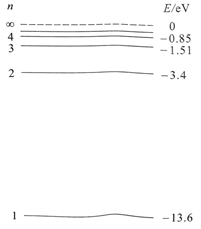
$\text{A.}$ $n=2$ 和 $n=1$ 能级之间的跃迁
$\text{B.}$ $n=3$ 和 $n=1$ 能级之间的跃迁
$\text{C.}$ $n=3$ 和 $n=2$ 能级之间的跃迁
$\text{D.}$ $n=4$ 和 $n=2$ 能级之间的跃迁
2022 年 12 月 8 日, 地球恰好运行到火星和太阳之间, 且三者几乎排成一条直线, 此现象被称为“火星冲日”。火星和地球几乎在同一平面内沿同一方向绕太阳做圆周运 动, 火星与地球的公转轨道半径之比约为 $3: 2$, 如图所示。根据以上信息可以得出
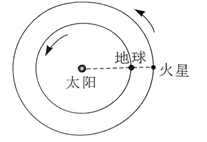
$\text{A.}$ 火星与地球绕太阳运动的周期之比约为$27:8$
$\text{B.}$ 当火星与地球相距最远时，两者的相对速度最大
$\text{C.}$ 火星与地球表面的自由落体加速度大小之比约为 $9:4$
$\text{D.}$ 下一次“火星冲日”将出现在2023年12月8日之前
在正点电荷 $\mathrm{Q}$ 产生的电场中有 $M 、 N$ 两点, 其电势分别为 $\varphi_M 、 \varphi_{\mathrm{N}}$, 电场强度大小分 别为 $E_{\mathrm{M}} 、 E_{\mathrm{N}}$ 。下列说法正确的是
$\text{A.}$ 若 $\varphi_{\mathrm{M}}>\varphi_{\mathrm{N}}$, 则 $M$ 点到电荷 $Q$ 的距离比 $N$ 点的远
$\text{B.}$ 若 $E_{\mathrm{M}} < E_{\mathrm{N}}$, 则 $M$ 点到电荷 $Q$ 的距离比 $N$ 点的近
$\text{C.}$ 若把带负电的试探电荷从 $M$ 点移到 $N$ 点, 电场力做正功, 则 $\varphi_M < \varphi_{\mathrm{N}}$
$\text{D.}$ 若把带正电的试探电荷从 $M$ 点移到 $N$ 点, 电场力做负功, 则 $E_{\mathrm{M}}>E_{\mathrm{N}}$
两节动车的额定功率分别为 $P_1$ 和 $P_2$, 在某平直铁轨上能达到的最大速度分别为 $v_1$ 和 $v_2$ 。现将它们编成动车组, 设每节动车运行时受到的阻力在编组前后不变, 则该动车 组在此铁轨上能达到的最大速度为
$\text{A.}$ $\frac{P_1 v_1+P_2 v_2}{P_1+P_2}$
$\text{B.}$ $\frac{P_1 v_2+P_2 v_1}{P_1+P_2}$
$\text{C.}$ $\frac{\left(P_1+P_2\right) v_1 v_2}{P_1 v_1+P_2 v_2}$
$\text{D.}$ $\frac{\left(P_1+P_2\right) v_1 v_2}{P_1 v_2+P_2 v_1}$
近场通信 ( $\mathrm{NFC})$ 器件应用电磁感应原理进行通讯, 其天线类似一个压平的线圈, 线圈尺寸从内到外逐渐变大。如图所示, 五正方形 $\mathrm{NFC}$ 线圈共 3 匝, 其边长分别为 $1.0 \mathrm{~cm} 、 1.2 \mathrm{~cm}$ 和 $1.4 \mathrm{~cm}$, 图中线圈外线接入内部芯片时与内部线圈绝缘。若匀强磁场 垂直通过此线圈, 磁感应强度变化率为 $10^3 \mathrm{~T} / \mathrm{s}$, 则线圈产生的感应电动势最接近
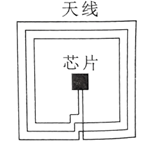
$\text{A.}$ 0.30v
$\text{B.}$ 0.44v
$\text{C.}$ 0.59v
$\text{D.}$ 43v
如图所示, 契形玻璃的横截面 $P O Q$ 的顶角为 $30^{\circ}, O P$ 边上的点光源 $S$ 到顶点 $O$ 的 距离为 $d$, 垂直于 $O P$ 边的光线 $S N$ 在 $O Q$ 边的折射角为 $45^{\circ}$ 。不考虑多次反射, $O Q$ 边 上有光射出部分的长度为
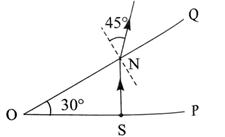
$\text{A.}$ $\frac{1}{2} d$
$\text{B.}$ $\frac{\sqrt{2}}{2} d$
$\text{C.}$ $d$
$\text{D.}$ $\sqrt{2} d$
一列简谐横波沿 $x$ 轴正向传播, 波长为 $100 \mathrm{~cm}$, 振幅为 $8 \mathrm{~cm}$ 。介质中有 $a$ 和 $b$ 两个 质点, 其平衡位置分别位于 $x=-\frac{40}{3} \mathrm{~cm}$ 和 $x=120 \mathrm{~cm}$ 处。某时刻 $b$ 质点的位移为 $y=4 \mathrm{~cm}$, 且向 $y$ 轴正方向运动。从该时刻开始计时, $a$ 质点的振动图像为
$\text{A.}$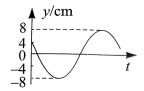 
$\text{B.}$ 
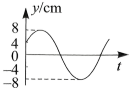$\text{C.}$ 
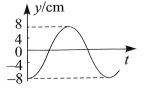$\text{D.}$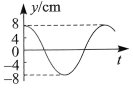 
多选题 （共 3 题 ），每题有多个选项正确
$t=0$ 时刻, 质点 $P$ 从原点由静止开始做直线运动, 其加速度 $a$ 随时间 $t$ 按图示的正 弦曲线变化, 周期为 $2 t_0$ 。在 $0 \sim 3 t_0$ 时间内, 下列说法正确的是
$\text{A.}$ $t=2 t_0$ 时, $P$ 回到原点
$\text{B.}$ $t=2 t_0$ 时, $P$ 的运动速度最小
$\text{C.}$ $t=t_0$ 时, $P$ 到原点的距离最远
$\text{D.}$ $t=\frac{3}{2} t_0$ 时, $P$ 的运动速度与 $t=\frac{1}{2} t_0$ 时相同
如图所示, 原长为 $l$ 的轻质弹簧, 一端固定在 $O$ 点, 另一端与二质量为 $m$ 的小球相 连。小球套在坚直固定的粗䊁杆上, 与杆之间的动摩擦因数为 0.5 。杆上 $M 、 N$ 两点与 $O$ 点的距离均为 $l, P$ 点到 $O$ 点的距离为 $\frac{1}{2} l, O P$ 与杆垂直。当小球置于杆上 $P$ 点时恰 好能保持静止。设最大静摩擦力等于滑动摩擦力, 重力加速度大小为 $g$ 。小球以某一 初速度从 $M$ 点向下运动到 $N$ 点, 在此过程中, 弹簧始终在弹性限度内。下列说法正确 的是
$\text{A.}$ 弹簧的劲度系数为 $\frac{4 m g}{l}$
$\text{B.}$ 小球在 $P$ 点下方 $\frac{1}{2} l$ 处的加速度大小为 $(3 \sqrt{2}-4) g$
$\text{C.}$ 从 $M$ 点到 $N$ 点的运动过程中, 小球受到的摩擦力先变小再变大
$\text{D.}$ 从 $M$ 点到 $P$ 点和从 $P$ 点到 $N$ 点的运动过程中, 小球受到的摩擦力做功相同
一带正电微粒从静止开始经电压 $U_1$ 加速后, 射入水平放置的平行板电容器, 极板 间电压为 $U_2$ 。微粒射入时紧靠下极板边缘, 速度方向与极板夹角为 $45^{\circ}$, 微粒运动轨 迹的最高点到极板左右两端的水平距离分别为 $2 L$ 和 $L$, 到两极板距离均为 $d$, 如图所 示。忽略边缘效应, 不计重力。下列说法正确的是
$\text{A.}$ $L: d=2: 1$
$\text{B.}$ $U_1: U_2=1: 1$
$\text{C.}$ 微粒穿过电容器区域的偏转角度的正切值为 2
$\text{D.}$ 仅改变微粒的质量或者电荷数量, 微粒在电容器中的运动轨迹不变
填空题 （共 2 题 ），请把答案直接填写在答题纸上
某同学利用测质量的小型家用电子秤, 设计了测量木块和木板间动摩擦因数 $\mu$ 的 实验。
如图 (a) 所示, 木板和木块 $\mathrm{A}$ 放在水平桌面上, 电子秤放在水平地面上, 木块 $\mathrm{A}$ 和 放在电子秤上的重物 B 通过跨过定滑轮的轻绳相连。调节滑轮, 使其与木块 $A$ 间的轻 绳水平, 与重物 $\mathrm{B}$ 间的轻绳坚直。在木块 $\mathrm{A}$ 上放置 $n(n=0,1,2,3,4,5)$ 个砝码（电子 秤称得每个砝码的质量 $m_0$ 为 $20.0 \mathrm{~g}$ ), 向左拉动木板的同时, 记录电子秤的对应示数 $m_{\circ}$
(1) 实验中, 拉动木板时 (填“必须”或“不必”) 保持匀速。
(2) 用 $m_{\mathrm{A}}$ 和 $m_{\mathrm{B}}$ 分别表示木块 $\mathrm{A}$ 和重物 $\mathrm{B}$ 的质量, 则 $m$ 和 $m_{\mathrm{A}} 、 m_{\mathrm{B}} 、 m_0 、 \mu 、 n$ 所满足 的关系式为 $m=$
(3) 根据测量数据在坐标纸上绘制出 $m-n$ 图像, 如图 (b) 所示, 可得木块 $A$ 和木板 间的动摩擦因数 $\mu=$ (保留 2 位有效数字)。
某实验小组为测量干电池的电动势和内阻, 设计了如图 (a) 所示电路, 所用器材如 下:
电压表 (量程 $0 \sim 3 \mathrm{~V}$, 内阻很大);
电流表 (量程0 0.6A);
电阻箱 (阻值 $0 \sim 999.9 \Omega$ );
干电池一节、开关一个和导线若干。
(1) 根据图 (a), 完成图 (b) 中的实物图连线 ________
（2）调节电阻箱到最大阻值, 闭合开关。逐次改变电阻箱的电阻, 记录其阻值 $R$ 、相 应的电流表示数 $I$ 和电压表示数 $U$ 。根据记录数据作出的 $U-I$ 图像如图 (c) 所示, 则 干电池的电动势为 ________ $\mathrm{V}$ (保留 3 位有效数字)、内阻为 ________ $\Omega$ (保留 2 位有效数字)。
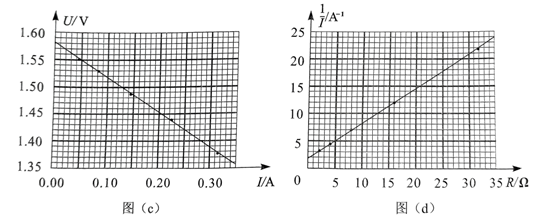
(3) 该小组根据记录数据进一步探究, 作出 $\frac{1}{I}-R$ 图像如图 (d) 所示。利用图 (d) 中图像的纵轴截距, 结合 (2) 问得到的电动势与内阻, 还可以求出电流表内阻为 ________ $\Omega$ (保留 2 位有效数字)。
(4) 由于电压表内阻不是无穷大, 本实验干电池内阻的测量值 ________ (填“偏大” 或“偏小”)。
解答题 （共 3 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
如图所示, 坚直放置在水平桌面上的左右两汽缸粗细均匀, 内壁光滑, 横截面积 分别为 $S 、 2 S$, 由体积可忽略的细管在底部连通。两汽缸中各有一轻质活塞将一定质 量的理想气体封闭, 左侧汽缸底部与活塞用轻质细弹簧相连。初始时, 两汽缸内封闭 气柱的高度均为 $H$, 弹簧长度恰好为原长。现往右侧活塞上表面缓慢添加一定质量的 沙子, 直至右侧活塞下降 $\frac{1}{3} H$, 左侧活塞上升 $\frac{1}{2} H$ 。已知大气压强为 $p_0$, 重力加速度 大小为 $g$, 汽缸足够长, 汽缸内气体温度始终不变, 弹簧始终在弹性限度内。求
（1）最终汽缸内气体的压强。
（2）弹簧的劲度系数和添加的沙子质量。
如图为某游戏装置原理示意图。水平桌面上固定云半圆形坚直挡板, 其半径为
$2 R$ 、内表面光滑, 挡板的两端 $A 、 B$ 在桌面边缘, $B$ 与半径为 $R$ 的固定光滑圆弧轨道 $\overparen{C D E}$ 在同一坚直平面内, 过 $C$ 点的轨道半径与坚直方向的夹角为 $60^{\circ}$ 。小物块以某一 水平初速度由 $A$ 点切入挡板内侧, 从 $B$ 点飞出桌面后, 在 $C$ 点沿圆弧切线方向进入轨 道 $\overparen{C D E}$ 内侧, 并恰好能到达轨道的最高点 $D$ 。小物块与桌面之间的动摩擦因数为 $\frac{1}{2 \pi}$, 重力加速度大小为 $g$, 忽略空气阻力, 小物块可视为质点。求:
（1）小物块到达 $D$ 点的速度大小;
(2) $B$ 和 $D$ 两点的高度差;
(3) 小物块在 $A$ 点的初速度大小。
如图所示, 空间存在磁感应强度大小为 $B$ 、垂直于 $x O y$ 平面向里的匀强磁场。 $t=0$ 时 刻, 一带正电粒子甲从点 $P(2 a, 0)$ 沿 $y$ 轴正方向射入, 第一次到达点 $O$ 时与运动到 该点的带正电粒子乙发生正碰。碰撞后, 粒子甲的速度方向反向、大小变为碰前的 3 倍, 粒子甲运动一个圆周时, 粒子乙刚好运动了两个圆周。已知粒子甲的质量为 $m$, 两粒子所带电荷量均为 $q$ 。假设所有碰撞均为弹性正碰, 碰撞时间忽略不计, 碰撞过 程中不发生电荷转移, 不考虑重力和两粒子间库仑力的影响。求:
（1）第一次碰撞前粒子甲的速度大小;
（2）粒子乙的质量和第一次碰撞后粒子乙的速度大小;
(3) $t=\frac{18 \pi m}{q B}$ 时刻粒子甲、乙的位置坐标, 及从第一次碰撞到 $t=\frac{18 \pi m}{q B}$ 的过程中粒子 乙运动的路程。(本小问不要求写出计算过程, 只写出答案即可)