单选题 （共 10 题 ），每题只有一个选项正确
-2023 的倒数是
$\text{A.}$ $2023$
$\text{B.}$ $-\frac{1}{2023}$
$\text{C.}$ $\frac{1}{2023}$
$\text{D.}$ $|2023|$
数学世界奇妙无穷, 其中曲线是微分几何的研究对象之一, 下列数学曲线既是轴对称图形, 又是中心对称图形的是
$\text{A.}$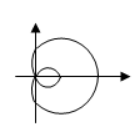 
$\text{B.}$ 
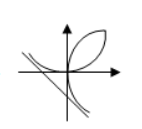$\text{C.}$ 
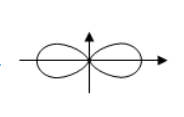$\text{D.}$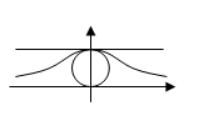 
根据今年的政府工作报告, 2023 年经济形势明显成上升势头, 城镇新增就业目标为 1200 万人左右, 1200 万用科学记数 法表示为
$\text{A.}$ $12 \times 10^6$
$\text{B.}$ $1.2 \times 10^6$
$\text{C.}$ $1.2 \times 10^7$
$\text{D.}$ $1200 \times 10^4$
下列计算正确的是
$\text{A.}$ $6 a b-3 a=3 b$
$\text{B.}$ $\left(-3 a^2 b\right)^2=6 a^4 b^2$
$\text{C.}$ $(a-1)^2=a^2-1$
$\text{D.}$ $5 a^2 b \div b=5 a^2$
一组数据: $3,4,4,4,5$, 下列对这组数据的统计量说法错误的是
$\text{A.}$ 平均数是 4
$\text{B.}$ 中位数是 4
$\text{C.}$ 方差是 4
$\text{D.}$ 众数是 4
下列选项中的尺规作图, 能推出 $ P A=P C $ 是
$\text{A.}$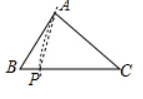 
$\text{B.}$ 
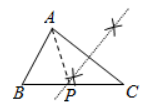$\text{C.}$ 
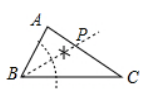$\text{D.}$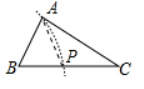 
下列命题正确的是
$\text{A.}$ 若 $a>b$, 则 $a-1 < b-1$
$\text{B.}$ 若 $(2,3)$ 是反比例函数 $y=\frac{k}{x}$ 图象上的点, 则 $(-1,6)$ 也是该函数图象上的点
$\text{C.}$ 矩形对角线相互平分且相等
$\text{D.}$ 三角形的一条中位线等分该三角形的面积
《算法统宗》是我国明代数学家程大位的主要著作在这部著作中, 许多数学问题都是以歌诀形式呈现的. “甜果苦果” 就是其中一首. “九百九十九文钱, 甜果苦果买一千, 四文钱买苦果七,十一文钱九个甜, 甜苦两果各几个? 请君布算莫迟疑! ”大 意是说: 用 999 文钱共买了 1000 个甜果和苦果, 其中 4 文钱可以买苦果 7 个, 11 文钱可以买甜果 9 个, 请问甜、苦果各买几个? 若设 苦果买 $x$ 个, 买甜果 $y$ 个, 可以列方程为
$\text{A.}$ $\left\{\begin{array}{l}x+y=999 \\ \frac{4}{7} x+\frac{11}{9} y=1000\end{array}\right.$
$\text{B.}$ $\left\{\begin{array}{l}x+y=1000 \\ \frac{7}{4} x+\frac{9}{11} y=999\end{array}\right.$
$\text{C.}$ $\left\{\begin{array}{l}x+y=1000 \\ \frac{4}{7} x+\frac{11}{9} y=999\end{array}\right.$
$\text{D.}$ $\left\{\begin{array}{l}x+y=999 \\ \frac{7}{4} x+\frac{9}{11} y=1000\end{array}\right.$
如图, $C D$ 为 $\odot O$ 直径, 弦 $A B \perp C D$ 且过半径 $O D$ 的中点 $H$, 过点 $A$ 的切线交 $C D$ 的延长线于 $G$, 且 $G H=6$, 点 $E$ 为 $\odot O$ 上一动点, $C F \perp A E$ 于点 $F$, 当点 $E$ 从点 $B$ 出发逆时针运动到点 $C$ 时, 点 $F$ 经过的路径长是
$\text{A.}$ $\frac{4}{3} \pi$
$\text{B.}$ $\frac{4 \sqrt{3}}{3} \pi$
$\text{C.}$ $\frac{8 \sqrt{3}}{3} \pi$
$\text{D.}$ $2 \sqrt{3^\pi}$
填空题 （共 5 题 ），请把答案直接填写在答题纸上
关于 $x$ 的一元二次方程 $x^2+6 x-a=0$ 的一个根是 3 , 另一个根是 $b$, 则 $a+b=$
“湾区之光”摩天轮位于深圳市华侨城欢乐港湾内, 是深圳地标性建筑之一, 摩天轮采用了世界首创的鱼鳍状异形大立 架, 有 28 个进口轿厢, 每个轿厢可容纳 25 人. 小亮在轿厢 $B$ 处看摩天轮的圆心 $O$ 处的仰角为 $30^{\circ}$, 看地面 $A$ 处的俯角为 $45^{\circ}$ (如图所 示, $O A$ 垂直于地面), 若摩天轮的半径为 54 米, 则此时小亮到地面的距离 $B C$ 为 米. ( 结果保留根号)
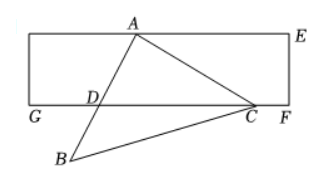
将等腰直角三角形 $\triangle A B C$ 纸片和矩形纸片按如图方式疍放在一起, 若 $A B$ 中点 $D$ 刚 好落在矩形纸片的边 $F G$ 上, 已知矩形纸片的边 $E F$ 长为 4 , 则 $B C$ 的长为
如图, 将 $\square A B C D$ 绕点 $A$ 逆时针旋转到 $\square A B^{\prime} C^{\prime} D^{\prime}$ 的位置使点 $B^{\prime}$ 落在 $B C$ 上, $B^{\prime} C^{\prime}$ 与 $C D$ 交于点 $E, D C^{\prime}$ 与 $B C$ 的延长线交于点 $F, A E$ 的延长线与 $B C$ 的延长线交于点 $G$, 若 $A B=3, B C=4, B B^{\prime}$ $=1$, 则 $F G$ 的长为
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(\sqrt{5}+1)^0+(-1)^{2023}+\left|-\sqrt{2} \sin 45^{\circ}\right|-\left(\frac{1}{3}\right)^{-1}$.
先化简, 再求值 $\left(1+\frac{4}{x-3}\right) \div \frac{x^2+2 x+1}{2 x-6}$, 其中 $x=\sqrt{2}-1$.
4月17日是“世界血友病日”, 某高校开展义务献血活动, 经过检测, 献血者血型有“ $A$, $B, A B, O$ ”四种类型, 随机抽取部分献血结果统计, 根据结果制作如图两幅不完整统计图表:
(1) 本次随机抽取献血者人数为 ________ 人, 图中 $m=20$;
( 2 ) 补全表中的数据;
(3) 若该高校总共有 2 万名学生, 估计其中 $A$ 型血的学生有 ________ 人；
(4) 现有 4 个自愿献血者, 2 人为 $O$ 型, 1 人为 $A$ 型, 1 人为 $B$ 型, 若在 4 人中随机挑选 2 人, 利用树状图或列表法求两人血型均为 $O$ 型的 概率.
应用题：深圳某学校为构建书香校园, 拟购进甲、乙两种规格的书柜放置新购置的图书. 已知每个甲种书柜的进价 比每个乙种书柜的进价高 $10 \%$, 用 3300 元购进的甲种书柜的数量比用 4500 元购进的乙种书柜的数量少 5 台.
（1）求甲、乙两种书柜的进价;
（2）若该校拟购进这两种规格的书柜共 60 个, 其中乙种书柜的数量不大于甲种书柜数量的 2 倍. 请您帮该校设计一种购买方案, 使得花费最少, 并求出最少花费多少钱.
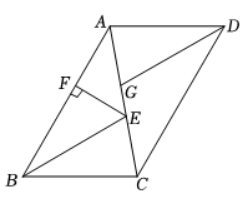
如图, 在 $\square A B C D$ 中, $B E 、 D G$ 分别平分 $\angle A B C 、 \angle A D C$, 交 $A C$ 于点 $E 、 G$.
(1) 求证: $B E / / D G, B E=D G$;
( 2 ) 过点 $E$ 作 $E F \perp A B$, 垂足为 $F$. 若 $\square A B C D$ 的周长为 $56, E F=6$, 求 $\triangle A B C$ 的面积.
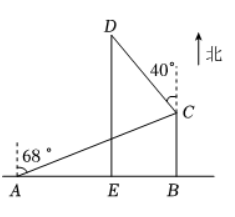
如图, $A B$ 为东西走向的滨海大道, 小莉沿滨海大道参加“低碳生活·绿色出行”健步走公益 活动. 小莉在点 $A$ 处时, 某艘海上观光船位于小莉北偏东 $68^{\circ}$ 的点 $C$ 处, 观光船到滨海大道的距离 $C B$ 为 $200 m$. 当小莉沿滨海大道向东步行 $200 m$ 到达点 $E$ 时, 观光船沿北偏西 $40^{\circ}$ 的方向航行至点 $D$ 处, 此时, 观光船恰好在小莉的正北方向, 求观光船从 $C$ 处航行到 $D$ 处的距离. (结果保留一位小数；参考数据: $\sin 40^{\circ} \approx 0.64, \cos 40^{\circ} \approx 0.77, \tan 40^{\circ} \approx 0.84, \sin 68^{\circ} \approx 0.93, \cos 68^{\circ} \approx 0.37, \tan 68^{\circ} \approx 2.48$ )
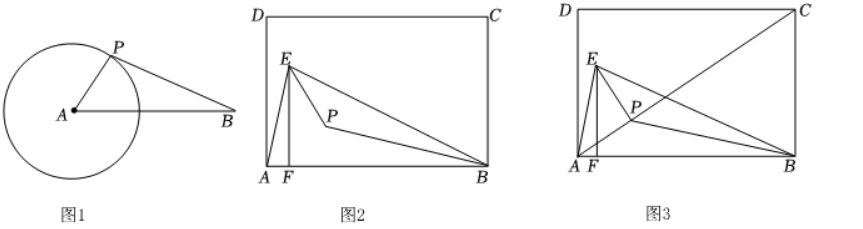
( 1 ) 如图 1, $\odot A$ 的半径为 $2, A B=5$, 点 $P$ 为 $\odot A$ 上任意一点, 则 $B P$ 的最小值为 3 .
( 2 ) 如图 2, 已知矩形 $A B C D$, 点 $E$ 为 $A B$ 上方一点, 连接 $A E, B E$, 作 $E F \perp A B$ 于点 $F$, 点 $P$ 是 $\triangle B E F$ 的内心, 求 $\angle B P E$ 的度数.
( 3 ) 如图 3 , 在 ( 2 ) 的条件下, 连接 $A P, C P$, 若矩形的边长 $A B=6, B C=4, B E=B A$, 求此时 $C P$ 的最小值.
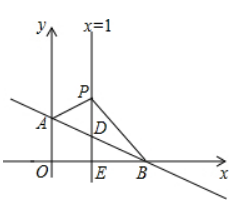
如图, 平面直角坐标系中, 直线 $A B: y=-\frac{1}{3} x+b$ 交 $y$ 轴于点 $A(0,1)$, 交 $x$ 轴于 点 $B$. 直线 $x=1$ 交 $A B$ 于点 $D$, 交 $x$ 轴于点 $E, P$ 是直线 $x=1$ 上一动点, 且在点 $D$ 的上方, 设 $P(1, n)$.
(1) 求直线 $A B$ 的解析式和点 $B$ 的坐标;
(2) 求 $\triangle A B P$ 的面积 (用含 $n$ 的代数式表示) ;
( 3 ) 当 $S_{\triangle A B P}=2$ 时, 以 $P B$ 为边在第一象限作等腰直角三角形 $B P C$, 求出点 $C$ 的坐标.
