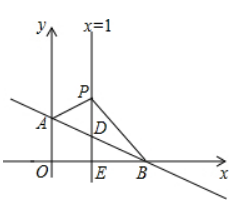
如图, 平面直角坐标系中, 直线 $A B: y=-\frac{1}{3} x+b$ 交 $y$ 轴于点 $A(0,1)$, 交 $x$ 轴于 点 $B$. 直线 $x=1$ 交 $A B$ 于点 $D$, 交 $x$ 轴于点 $E, P$ 是直线 $x=1$ 上一动点, 且在点 $D$ 的上方, 设 $P(1, n)$.
(1) 求直线 $A B$ 的解析式和点 $B$ 的坐标;
(2) 求 $\triangle A B P$ 的面积 (用含 $n$ 的代数式表示) ;
( 3 ) 当 $S_{\triangle A B P}=2$ 时, 以 $P B$ 为边在第一象限作等腰直角三角形 $B P C$, 求出点 $C$ 的坐标.