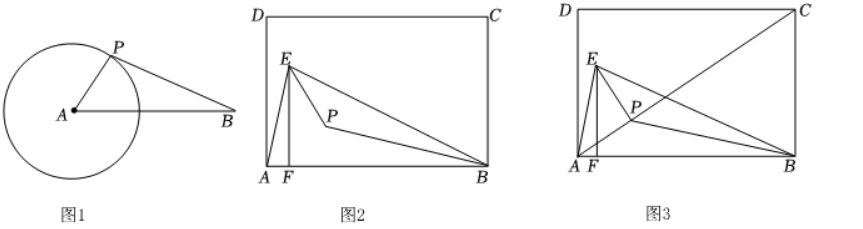
( 1 ) 如图 1, $\odot A$ 的半径为 $2, A B=5$, 点 $P$ 为 $\odot A$ 上任意一点, 则 $B P$ 的最小值为 3 .
( 2 ) 如图 2, 已知矩形 $A B C D$, 点 $E$ 为 $A B$ 上方一点, 连接 $A E, B E$, 作 $E F \perp A B$ 于点 $F$, 点 $P$ 是 $\triangle B E F$ 的内心, 求 $\angle B P E$ 的度数.
( 3 ) 如图 3 , 在 ( 2 ) 的条件下, 连接 $A P, C P$, 若矩形的边长 $A B=6, B C=4, B E=B A$, 求此时 $C P$ 的最小值.
( 2 ) 如图 2, 已知矩形 $A B C D$, 点 $E$ 为 $A B$ 上方一点, 连接 $A E, B E$, 作 $E F \perp A B$ 于点 $F$, 点 $P$ 是 $\triangle B E F$ 的内心, 求 $\angle B P E$ 的度数.
( 3 ) 如图 3 , 在 ( 2 ) 的条件下, 连接 $A P, C P$, 若矩形的边长 $A B=6, B C=4, B E=B A$, 求此时 $C P$ 的最小值.
