单选题 (共 14 题 ),每题只有一个选项正确
某质点作直线运动的运动学方程为 $x=3 t-5 t^3+6 $, 则该质点作
$\text{A.}$ 匀加速直线运动, 加速度沿 $x$ 轴正方向.
$\text{B.}$ 匀加速直线运动, 加速度沿 $x$ 轴负方向.
$\text{C.}$ 变加速直线运动, 加速度沿 $x$ 轴正方向.
$\text{D.}$ 变加速直线运动, 加速度沿 $x$ 轴负方向.
一质点在平面上运动, 已知质点位置矢量的表示式为 $\vec{r}=a t^2 \vec{i}+b t^2 \vec{j}$ (其中 $a 、 b$ 为常量), 则该质点作
$\text{A.}$ 匀速直线运动.
$\text{B.}$ 变速直线运动.
$\text{C.}$ 抛物线运动.
$\text{D.}$ 一般曲线运动.
一运动质点在某瞬时位于矢径 $\vec{r}(x, y)$ 的端点处, 其速度大小为
$\text{A.}$ $\frac{d r}{d t}$
$\text{B.}$ $\frac{\mathrm{d} \vec{r}}{\mathrm{~d} t}$
$\text{C.}$ $\frac{\mathrm{d} \vec{r} \mid}{\mathrm{d} t}$
$\text{D.}$ $\sqrt{\left(\frac{d x}{d t}\right)^2+\left(\frac{d y}{d t}\right)^2}$
对于沿曲线运动的物体, 以下几种说法中哪一种是正确的
$\text{A.}$ 切向加速度必不为零.
$\text{B.}$ 法向加速度必不为零 (拐点处除外).
$\text{C.}$ 由于速度沿切线方向, 法向分速度必为零, 因此法向加速度必为零.
$\text{D.}$ 若物体作匀速率运动, 其总加速度必为零.
$\text{E.}$ 若物体的加速度 $\vec{a}$ 为恒矢量, 它一定作匀变速率运动.
一个质点在做匀速率圆周运动时
$\text{A.}$ 切向加速度改变,法向加速度也改变
$\text{B.}$ 切向加速度不变,法向加速度改变
$\text{C.}$ 切向加速度不变,法向加速度也不变
$\text{D.}$ 切向加速度改变,法向加速度不变
在高台上分别沿45°仰角方向和水平方向,以同样速率投出两颗小石子,忽略空气阻力,则它们落地时速度
$\text{A.}$ 大小不同,方向不同
$\text{B.}$ 大小相同,方向不同
$\text{C.}$ 大小相同,方向相同
$\text{D.}$ 大小不同,方向相同
某人骑自行车以速率v向西行驶,今有风以相同速率从北偏东30°方向吹来,试问人感到风从哪个方向吹来?
$\text{A.}$ 北偏东30°
$\text{B.}$ 南偏东30°
$\text{C.}$ 北偏西30°
$\text{D.}$ 西偏南30°
图中p是一圆的竖直直径pc的上端点,一质点从p开始分别沿不同的弦无摩擦下滑时,到达各弦的下端所用的时间相比较是
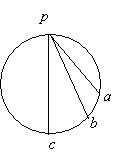
$\text{A.}$ 到a用的时间最短
$\text{B.}$ 到b用的时间最短
$\text{C.}$ 到c用的时间最短
$\text{D.}$ 所用时间都一样
一条河在某一段直线岸边同侧有A、B两个码头,相距1 km.甲、乙两人需要从码头A到码头B,再立即由B返回.甲划船前去,船相对河水的速度为4 km/h;而乙沿岸步行,步行速度也为4 km/h.如河水流速为2 km/h,方向从A到B,则
$\text{A.}$ A.甲比乙晚10分钟回到A.
$\text{B.}$ 甲和乙同时回到A
$\text{C.}$ 甲比乙早10分钟回到A
$\text{D.}$ 甲比乙早2分钟回到A
质点作半径为R的变速圆周运动时的加速度大小为(v表示任一时刻质点的速率)
$\text{A.}$ $\frac{d t}{d t}$.
$\text{B.}$ $\frac{v^2}{R}$.
$\text{C.}$ $\frac{\mathrm{d} v}{\mathrm{~d} t}+\frac{v^2}{R}$.
$\text{D.}$ $\left[\left(\frac{d y}{d t}\right)^2+\left(\frac{y^4}{R^2}\right)\right]^{1 / 2}$
一运动质点在某瞬时位于矢径 $\vec{r}(x, y)$ 的端点处, 其速度大小为
$\text{A.}$ $\frac{d r}{d t}$
$\text{B.}$ $\frac{d \vec{r}}{d t}$
$\text{C.}$ $\frac{d|\vec{r}|}{d t}$
$\text{D.}$ $\sqrt{\left(\frac{d x}{d t}\right)^2+\left(\frac{d y}{d t}\right)^2}$
以下五种运动形式中, $\vec{a}$ 保持不变的运动是
$\text{A.}$ 单摆的运动.
$\text{B.}$ 匀速率圆周运动.
$\text{C.}$ 行星的椭圆轨道运动.
$\text{D.}$ 抛体运动.
$\text{E.}$ 圆锥摆运动.
一物体从某一确定高度以 ${v_0}$ 的速度水平抛出, 已知它落地时的速度为 ${v_t}$, 那么它运动的时间是
$\text{A.}$ $\frac{y_t-y_0}{g}$.
$\text{B.}$ $\frac{y_t-y_0}{2 g}$.
$\text{C.}$ $\left(v_t^2-v_0^2\right)^{1 / 2}$
$\text{D.}$ $\frac{\left(v_t^2-y_0^2\right)^{1 / 2}}{2 g}$
一质点沿 $x$ 轴作直线运动, 其 $v-t$ 曲线如图所示, 如 $t=0$ 时, 质点位于坐标原点, 则 $t=4.5 \mathrm{~s}$ 时, 质点在 $x$ 轴上的位置为
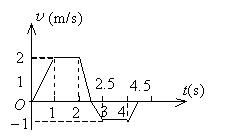
$\text{A.}$ $5 \mathrm{~m}$
$\text{B.}$ $2 \mathrm{~m}$
$\text{C.}$ 0
$\text{D.}$ $-2 \mathrm{~m}$
$\text{E.}$ $-5 \mathrm{~m}$
填空题 (共 15 题 ),请把答案直接填写在答题纸上
一质点沿 $x$ 方向运动, 其加速度随时间变化关系为 $a=3+2 t(\mathrm{SI})$, 如果初始时质点的速度 $v_0$ 为 $5 \mathrm{~m} / \mathrm{s}$, 则当 $t$ 为 $3 \mathrm{~s}$ 时, 质点的速度 $v=$
3
一辆作匀加速直线运动的汽车,在6s内通过相隔60 m远的两点,已知汽车经过第二点时的速率为15m/s,则
(1)汽车通过第一点时的速率v1=________;
(2)汽车的加速度a=________.
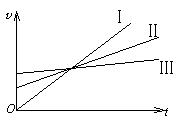
在$v-t$图中所示的三条直线都表示同一类型的运动:
(1)Ⅰ、Ⅱ、Ⅲ三条直线表示的是________运动;
(2)________线所表示的运动的加速度最大.
一质点作半径为 $0.1 \mathrm{~m}$ 的圆周运动, 其角位置的运动学方程为:
$
\theta=\frac{\pi}{4}+\frac{1}{2} t^2
$
则其切向加速度为 ${a_t}=$
试说明质点作何种运动时, 将出现下述各种情况 $(v \ne 0)$
(1) $a_t \neq 0, a_n \neq 0$
(1) $a_t \neq 0, a_n = 0$
$a_t 、 a_n$ 分别表示切向加速度和法向加速度。
有一旅客站在沿水平轨道匀速开行的列车最后一节车厢后的平台上,
(1)手拿石块,松手释放;
(2)沿水平方向向车后掷出石块,使石块相对车的速度等于火车相对于地的速度.
则站在铁路路基旁的观察者所见石块的运动是:
一质点沿 $\mathrm{x}$ 轴运动, 其加速度为 $\mathrm{a}=4 \mathrm{t}(\mathrm{SI})$, 已知 $\mathrm{t}=0$ 时, 质点位于 $x_0=10 \mathrm{~m}$ 处, 初速度 $v_0=0$, 试求其位置和时间的关 系式
有一质点沿 $x$ 轴作直线运动, $t$ 时刻的坐标为 $x=4.5 t^2-2 t^3(\mathrm{SI})$. 试求:
(1)第 2 秒内的平均速度;
(2)第 2 秒末的瞬时速度;
(3)第 2 秒内的路程。
一质点沿半径为 $R$ 的圆周运动. 质点所经过的弧长与时间的关系为 $S=b t+\frac{1}{2} c t^2$ 其中 $b 、 c$ 是大于零的常量, 求从 $t=0$ 开始到切向加速度与法向加速度大小相等时所经历的时间。
当火车静止时,乘客发现雨滴下落方向偏向车头,偏角为30°,当火车以35 m/s的速率沿水平直路行驶时,发现雨滴下落方向偏向车尾,偏角为45°,假设雨滴相对于地的速度保持不变,试计算雨滴相对地的速度大小
一质点作直线运动,其坐标x与时间t的关系曲线如图所示.则该质点在第________
秒瞬时速度为零;在第________秒至第________秒间速度与加速度同方向.

在一个转动的齿轮上, 一个齿尖 $P$ 沿半径为 $R$ 的圆周运动, 其路程 $S$ 随时间的变化规律为 $S=v_0 t+\frac{1}{2} b t^2$, 其中 $v_0$ 和 $b$ 都是正的常量. 则 $t$ 时刻齿尖 $P$ 的速度大小为 , 加速度大小为
质点沿半径为 $R$ 的圆周运动, 运动学方程为 $\theta=3+2 t^2$ (SI), 则 $t$ 时刻质点的法向加速度大小为
$a_n=$ ;角加速度 $\beta=$
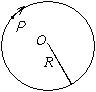
如图所示, 质点 $P$ 在水平面内沿一半径为 $R=2 \mathrm{~m}$ 的圆轨道转动. 转动的角速度与时间的函数关系为 $\omega=k t^2(k$ 为常 量). 已知 $t=2 s$ 时, 质点 $P$ 的速度值为 $32 \mathrm{~m} / \mathrm{s}$. 试求 $t=1$ 时, 质点 $P$ 的速度与加速度的大小.
已知质点的运动学方程为$\vec{r}=\left(5+2 t-\frac{1}{2} t^2\right) \vec{i}+\left(4 t+\frac{1}{3} t^3\right) \vec{j}$ 当t= 2 s时,加速度的大小为________;加速度$\vec{a}$与x轴正方向间夹角为