单选题 (共 8 题 ),每题只有一个选项正确
如图是某几何体的三视图,该几何体是( )
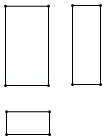
$\text{A.}$ 圆柱
$\text{B.}$ 圆椎
$\text{C.}$ 三棱柱
$\text{D.}$ 长方体
2020年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为( )
$\text{A.}$ $0.36 \times 10^{5}$
$\text{B.}$ $3.6 \times 10^{5}$
$\text{C.}$ $3.6 \times 10^{4}$
$\text{D.}$ $36 \times 10^{3}$
如图,AB和CD相交于点O,则下列结论正确的是( )
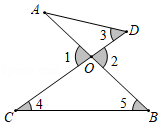
$\text{A.}$ $\angle 1=\angle 2$
$\text{B.}$ $\angle 2=\angle 3$
$\text{C.}$ $\angle 1>\angle 4+\angle 5$
$\text{D.}$ $\angle 2 < \angle 5$
下列图形中,既是中心对称图形也是轴对称图形的是( )
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
正五边形的外角和为( )
$\text{A.}$ $180^{\circ}$
$\text{B.}$ $360^{\circ}$
$\text{C.}$ $540^{\circ}$
$\text{D.}$ $720^{\circ}$
实数a在数轴上的对应点的位置如图所示,若实数b满足﹣a<b<a,则b的值可以是( )
$\text{A.}$ 2
$\text{B.}$ -1
$\text{C.}$ -2
$\text{D.}$ -3
不透明的袋子中有两个小球, 上面分别写着数字“ 1 ”, “ 2 ”, 除数字外两个小球无其他差别. 从 中随机摸出一个小球, 记录其数字, 放回并摇匀, 再从中随机摸出一个小球, 记录其数 字, 那么两次记录的数字之和为 3 的概率是( )
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{3}$
有一个装有水的容器,如图所示,容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )
$\text{A.}$ 正比例函数关系
$\text{B.}$ 一次函数关系
$\text{C.}$ 二次函数关系
$\text{D.}$ 反比例函数关系
填空题 (共 8 题 ),请把答案直接填写在答题纸上
若代数式 $\frac{1}{x-7}$ 有意义, 则实数 $x$ 的取值范围是( )
已知关于 $x$ 的方程 $x^{2}+2 x+k=0$ 有两个相等的实数根, 则 $k$ 的值是 ( )
写出一个比 $\sqrt{2}$ 大且比 $\sqrt{15}$ 小的整数
方程组$\left\{\begin{array}{l}
x-y=1 \\
3 x+y=7
\end{array}\right.$ 的解为 ( )
在平面直角坐标系 $x O y$ 中, 直线 $y=x$ 与双曲线 $y=\frac{m}{x}$ 交于 $A, B$ 两点. 若点 $A, B$ 的纵坐 标分别为 $y_{1}, y_{2}$, 则 $y_{1}+y_{2}$ 的值为 ( )
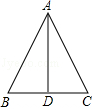
如图, 在 $\triangle A B C$ 中, $A B=A C$, 点 $D$ 在 $B C$ 上 (不与点 $B, C$ 重合). 只需添加一个条件即可 证明 $\triangle A B D \cong \triangle A C D$, 这个条件可以是 ( ) (写出一个即可).
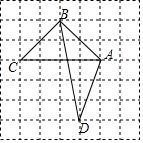
如图所示的网格是正方形网格, $A, B, C, D$ 是网格线交点, 则 $\triangle A B C$ 的面积与 $\triangle A B D$ 的面积的大小关系为: $S_{\triangle A B C} $ ( ) $ S_{\triangle A B D}$ (填 > = 或 < )
如图是某剧场第一排座位分布图. 甲、乙、丙、丁四人购票, 所购票数分别为 $2,3,4,5$. 每 人选座购票时, 只购买第一排的座位相邻的票, 同时使自己所选的座位号之和最小, 如 果按 “甲、乙、丙、丁”的先后顺序购票, 那么甲购买 1,2 号座位的票, 乙购买 3,5 , 7 号座位的票, 丙选座购票后, 丁无法购买到第一排座位的票. 若丙第一个购票, 要使其 他三人都能购买到第一排座位的票, 写出一种满足条件的购票的先后顺序

解答题 (共 12 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$\left(\frac{1}{3}\right)^{-1}+\sqrt{18}+|-2|-6 \sin 45^{\circ}$.
解不等式组: $\left\{\begin{array}{l}5 x-3>2 x, \\ \frac{2 x-1}{3} < \frac{x}{2} .\end{array}\right.$
已知 $5 x^{2}-x-1=0$, 求代数式 $(3 x+2)(3 x-2)+x(x-2)$ 的值.
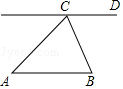
已知: 如图, $\triangle A B C$ 为锐角三角形, $A B=A C, C D / / A B$.
求作: 线段 $B P$, 使得点 $P$ 在直线 $C D$ 上, 且 $\angle A B P=\frac{1}{2} \angle B A C$.
作法: (1)以点 $A$ 为圆心, $A C$ 长为半径画圆, 交直线 $C D$ 于 $C, P$ 两点;
(2)连接 $B P$.
线段 $B P$ 就是所求作的线段.
(1) 使用直尺和圆规, 依作法补全图形 (保留作图痕迹);
(2) 完成下面的证明.
证明: $\because C D / / A B$,
$$
\therefore \angle A B P=
$$
$$
\because A B=A C \text {, }
$$
$\therefore$ 点 $B$ 在 $\odot A$ 上.
又 $\because$ 点 $C, P$ 都在 $\odot A$ 上,
$\therefore \angle B P C=\frac{1}{2} \angle B A C$ ( ) (填推理的依据).
$\therefore \angle A B P=\frac{1}{2} \angle B A C .$
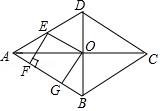
如图, 菱形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $O, E$ 是 $A D$ 的中点, 点 $F, G$ 在 $A B$ 上, $E F$
$\perp A B, O G / / E F$.
(1) 求证: 四边形 $O E F G$ 是矩形;
(2) 若 $A D=10, E F=4$, 求 $O E$ 和 $B G$ 的长.
在平面直角坐标系 $x O y$ 中, 一次函数 $y=k x+b(k \neq 0)$ 的图象由函数 $y=x$ 的图象平移得到,
且经过点 $(1,2)$.
(1)求这个一次函数的解析式;
(2) 当 $x>1$ 时, 对于 $x$ 的每一个值, 函数 $y=m x(m \neq 0)$ 的值大于一次函数 $y=k x+b$ 的值, 直接写出 $m$ 的取值范围.
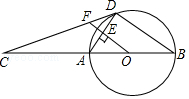
如图, $A B$ 为 $\odot O$ 的直径, $C$ 为 $B A$ 延长线上一点, $C D$ 是 $\odot O$ 的切线, $D$ 为切点, $O F \perp A D$ 于点 $E$, 交 $C D$ 于点 $F$.
(1) 求证: $\angle A D C=\angle A O F$;
(2) 若 $\sin C=\frac{1}{3}, B D=8$, 求 $E F$ 的长.
小云在学习过程中遇到一个函数 $y=\frac{1}{6}|x|\left(x^{2}-x+1\right)(x \geqslant-2)$.
下面是小云对其探究的过程, 请补充完整:
(1) 当 $-2 \leqslant x < 0$ 时, 对于函数 $y_{1}=|x|$, 即 $y_{1}=-x$, 当 $-2 \leqslant x < 0$ 时, $y_{1}$ 随 $x$ 的增大而 且 $y_{1}>0$; 对于函数 $y_{2}=x^{2}-x+1$, 当 $-2 \leqslant x < 0$ 时, $y_{2}$ 随 $x$ 的增大而 ( ) , 且 $y_{2}>0$; 结 合上述分析, 进一步探究发现, 对于函数 $y$, 当 $-2 \leqslant x < 0$ 时, $y$ 随 $x$ 的增大而
(2)当 $x \geqslant 0$ 时, 对于函数 $y$, 当 $x \geqslant 0$ 时, $y$ 与 $x$ 的几组对应值如下表:
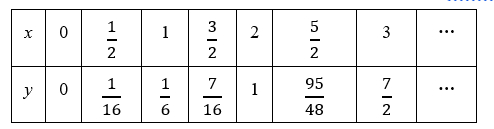
结合上表, 进一步探究发现, 当 $x \geqslant 0$ 时, $y$ 随 $x$ 的增大而增大. 在平面直角坐标系 $x O x$ 中, 画出当 $x \geqslant 0$ 时的函数 $y$ 的图象.
(3) 过点 $(0, m)(m>0)$ 作平行于 $x$ 轴的直线 $l$, 结合 (1) (2) 的分析, 解决问题 若直线 $l$ 与函数 $y=\frac{1}{6}|x|\left(x^{2}-x+1\right)(x \geqslant-2)$ 的图象有两个交点, 则 $m$ 的最大值是 ( )
小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
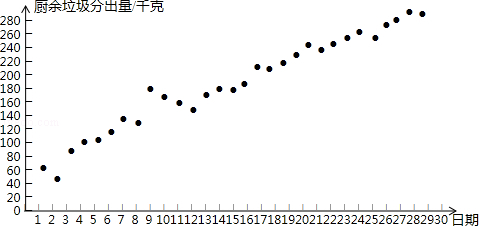
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:

(1) 该小区 5 月 1 日至 30 日的厨余垃圾分出量的平均数约为(结果取整数);
(2) 已知该小区 4 月的厨余垃圾分出量的平均数为 60 , 则该小区 5 月 1 日至 30 日的厨 余垃圾分出量的平均数约为 4 月的 ( ) 倍(结果保留小数点后一位);
(3) 记该小区 5 月 1 日至 10 日的厨余垃圾分出量的方差为 $s_{1}^{2}$ , 5 月 11 日至 20 日的厨余垃圾分出量的方差为 $s_{2}^{2}$,5 月 21 日至 30 日的厨余垃圾分出量的方差为 $s_{3}{ }^{2}$. 直接写出 $s_{1}^{2}, s_{2}^{2}, s_{3}^{2}$ 的大小关系.
在平面直角坐标系 $x O y$ 中, $M\left(x_{1}, y_{1}\right), N\left(x_{2}, y_{2}\right)$ 为抛物线 $y=a x^{2}+b x+c(a>0)$ 上任意 两点, 其中 $x_{1} < x_{2}$.
(1)若抛物线的对称轴为 $x=1$, 当 $x_{1}, x_{2}$ 为何值时, $y_{1}=y_{2}=c$;
(2)设抛物线的对称轴为 $x=t$, 若对于 $x_{1}+x_{2}>3$, 都有 $y_{1} < y_{2}$, 求 $t$ 的取值范围.
在 $\triangle A B C$ 中, $\angle C=90^{\circ}, A C>B C, D$ 是 $A B$ 的中点. $E$ 为直线 $A C$ 上一动点, 连接 $D E$. 过 点 $D$ 作 $D F \perp D E$, 交直线 $B C$ 于点 $F$, 连接 $E F$.
(1) 如图 1, 当 $E$ 是线段 $A C$ 的中点时, 设 $A E=a, B F=b$, 求 $E F$ 的长(用含 $a, b$ 的 式子表示);
(2)当点 $E$ 在线段 $C A$ 的延长线上时, 依题意补全图 2, 用等式表示线段 $A E, E F, B F$ 之间的数量关系, 并证明.

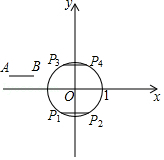
在平面直角坐标系 $x O y$ 中, $\odot O$ 的半径为 $1, A, B$ 为 $\odot O$ 外两点, $A B=1$.
给出如下定义: 平移线段 $A B$, 得到 $\odot O$ 的弦 $A^{\prime} B^{\prime}$ ( $A^{\prime}, B^{\prime}$ 分别为点 $A, B$ 的对应点), 线段 $A A^{\prime}$ 长度的最小值称为线段 $A B$ 到 $\odot O$ 的 “平移距离”.
(1) 如图, 平移线段 $A B$ 得到 $\odot O$ 的长度为 1 的弦 $P_{1} P_{2}$ 和 $P_{3} P_{4}$, 则这两条弦的位置关 系是 ( ) 在点 $P_{1}, P_{2}, P_{3}, P_{4}$ 中, 连接点 $A$ 与点 的线段的长度等于线段 $A B$ 到 $\odot O$ 的 “平移距离”;
(2) 若点 $A, B$ 都在直线 $y=\sqrt{3} x+2 \sqrt{3}$ 上, 记线段 $A B$ 到 $\odot O$ 的 “平移距离” 为 $d_{1}$, 求 $d_{1}$ 的最小值;
(3) 若点 $A$ 的坐标为 $\left(2, \frac{3}{2}\right)$, 记线段 $A B$ 到 $\odot O$ 的 “平移距离” 为 $d_{2}$, 直接写出 $d_{2}$ 的 取值范围.