在平面直角坐标系 $x O y$ 中, $\odot O$ 的半径为 $1, A, B$ 为 $\odot O$ 外两点, $A B=1$.
给出如下定义: 平移线段 $A B$, 得到 $\odot O$ 的弦 $A^{\prime} B^{\prime}$ ( $A^{\prime}, B^{\prime}$ 分别为点 $A, B$ 的对应点), 线段 $A A^{\prime}$ 长度的最小值称为线段 $A B$ 到 $\odot O$ 的 “平移距离”.
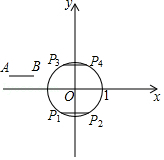
(1) 如图, 平移线段 $A B$ 得到 $\odot O$ 的长度为 1 的弦 $P_{1} P_{2}$ 和 $P_{3} P_{4}$, 则这两条弦的位置关 系是 ( ) 在点 $P_{1}, P_{2}, P_{3}, P_{4}$ 中, 连接点 $A$ 与点 的线段的长度等于线段 $A B$ 到 $\odot O$ 的 “平移距离”;
(2) 若点 $A, B$ 都在直线 $y=\sqrt{3} x+2 \sqrt{3}$ 上, 记线段 $A B$ 到 $\odot O$ 的 “平移距离” 为 $d_{1}$, 求 $d_{1}$ 的最小值;
(3) 若点 $A$ 的坐标为 $\left(2, \frac{3}{2}\right)$, 记线段 $A B$ 到 $\odot O$ 的 “平移距离” 为 $d_{2}$, 直接写出 $d_{2}$ 的 取值范围.
给出如下定义: 平移线段 $A B$, 得到 $\odot O$ 的弦 $A^{\prime} B^{\prime}$ ( $A^{\prime}, B^{\prime}$ 分别为点 $A, B$ 的对应点), 线段 $A A^{\prime}$ 长度的最小值称为线段 $A B$ 到 $\odot O$ 的 “平移距离”.
(1) 如图, 平移线段 $A B$ 得到 $\odot O$ 的长度为 1 的弦 $P_{1} P_{2}$ 和 $P_{3} P_{4}$, 则这两条弦的位置关 系是 ( ) 在点 $P_{1}, P_{2}, P_{3}, P_{4}$ 中, 连接点 $A$ 与点 的线段的长度等于线段 $A B$ 到 $\odot O$ 的 “平移距离”;
(2) 若点 $A, B$ 都在直线 $y=\sqrt{3} x+2 \sqrt{3}$ 上, 记线段 $A B$ 到 $\odot O$ 的 “平移距离” 为 $d_{1}$, 求 $d_{1}$ 的最小值;
(3) 若点 $A$ 的坐标为 $\left(2, \frac{3}{2}\right)$, 记线段 $A B$ 到 $\odot O$ 的 “平移距离” 为 $d_{2}$, 直接写出 $d_{2}$ 的 取值范围.
