已知: 如图, $\triangle A B C$ 为锐角三角形, $A B=A C, C D / / A B$.
求作: 线段 $B P$, 使得点 $P$ 在直线 $C D$ 上, 且 $\angle A B P=\frac{1}{2} \angle B A C$.
作法: (1)以点 $A$ 为圆心, $A C$ 长为半径画圆, 交直线 $C D$ 于 $C, P$ 两点;
(2)连接 $B P$.
线段 $B P$ 就是所求作的线段.
(1) 使用直尺和圆规, 依作法补全图形 (保留作图痕迹);
(2) 完成下面的证明.
证明: $\because C D / / A B$,
$$
\therefore \angle A B P=
$$
$$
\because A B=A C \text {, }
$$
$\therefore$ 点 $B$ 在 $\odot A$ 上.
又 $\because$ 点 $C, P$ 都在 $\odot A$ 上,
$\therefore \angle B P C=\frac{1}{2} \angle B A C$ ( ) (填推理的依据).
$\therefore \angle A B P=\frac{1}{2} \angle B A C .$
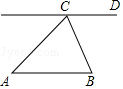
求作: 线段 $B P$, 使得点 $P$ 在直线 $C D$ 上, 且 $\angle A B P=\frac{1}{2} \angle B A C$.
作法: (1)以点 $A$ 为圆心, $A C$ 长为半径画圆, 交直线 $C D$ 于 $C, P$ 两点;
(2)连接 $B P$.
线段 $B P$ 就是所求作的线段.
(1) 使用直尺和圆规, 依作法补全图形 (保留作图痕迹);
(2) 完成下面的证明.
证明: $\because C D / / A B$,
$$
\therefore \angle A B P=
$$
$$
\because A B=A C \text {, }
$$
$\therefore$ 点 $B$ 在 $\odot A$ 上.
又 $\because$ 点 $C, P$ 都在 $\odot A$ 上,
$\therefore \angle B P C=\frac{1}{2} \angle B A C$ ( ) (填推理的依据).
$\therefore \angle A B P=\frac{1}{2} \angle B A C .$
