单选题 (共 23 题 ),每题只有一个选项正确
下列命题中正确的是
$\text{A.}$ 若函数 $f(x)$ 在 $x=x_0$ 处不可导, 则 $f(x)$ 在 $x=x_0$ 处不连续.
$\text{B.}$ 若函数 $f(x)$ 在 $x=x_0$ 处不连续, 则 $f_{-}^{\prime}\left(x_0\right), f_{+}^{\prime}\left(x_0\right)$ 中至少有一个不存在.
$\text{C.}$ 若 $f_{-}^{\prime}\left(x_0\right), f_{+}^{\prime}\left(x_0\right)$ 存在, 则函数 $f(x)$ 在 $x=x_0$ 处可导.
$\text{D.}$ 若函数 $f(x)$ 在 $x=x_0$ 处连续, 则 $f(x)$ 在 $x=x_0$ 处左可导并且右可导.
设 $f(x)$ 在点 $x=a$ 的某个邻域内有定义, 则 $f(x)$ 在 $x=a$ 处可导的一个充分条件是
$\text{A.}$ $\lim _{h \rightarrow+\infty} h\left[f\left(a+\frac{1}{h}\right)-f(a)\right]$ 存在.
$\text{B.}$ $\lim _{h \rightarrow 0} \frac{f(a+2 h)-f(a+h)}{h}$ 存在.
$\text{C.}$ $\lim _{h \rightarrow 0} \frac{f(a+h)-f(a-h)}{2 h}$ 存在.
$\text{D.}$ $\lim _{h \rightarrow 0} \frac{f(a)-f(a-h)}{h}$ 存在.
设函数 $f(x)=\lim _{n \rightarrow \infty} \sqrt[n]{1+|x|^{3 n}}$, 则 $f(x)$ 在 $(-\infty,+\infty)$ 内
$\text{A.}$ 处处可导.
$\text{B.}$ 恰有一个不可导点.
$\text{C.}$ 恰有两个不可导点.
$\text{D.}$ 至少有三个不可导点.
设函数 $f(x)$ 连续, 且 $f^{\prime}(0)>0$, 则存在 $\delta>0$, 使得
$\text{A.}$ $f(x)$ 在 $(0, \delta)$ 内单调增加.
$\text{B.}$ $f(x)$ 在 $(-\delta, 0)$ 内单调减少.
$\text{C.}$ 对任意的 $x \in(0, \delta)$, 有 $f(x)>f(0)$.
$\text{D.}$ 对任意的 $x \in(-\delta, 0)$, 有 $f(x)>f(0)$.
设函数 $f(x)$ 在 $x=0$ 的某邻域内连续, 且 $\lim _{x \rightarrow 0} \frac{f(x)}{x \sin x}=-2$, 则在 $x=0$ 处 $f(x)$
$\text{A.}$ 不可导.
$\text{B.}$ 可导, 且 $f^{\prime}(0) \neq 0$.
$\text{C.}$ 取极大值.
$\text{D.}$ 取极小值.
设函数 $f(x)$ 具有 2 阶导数, $g(x)=f(0)(1-x)+f(1) x$ 则在区间 $[0,1]$ 上
$\text{A.}$ 当 $f^{\prime}(x) \geq 0$ 时, $f(x) \geq g(x)$.
$\text{B.}$ 当 $f^{\prime}(x) \geq 0$ 时, $f(x) \leq g(x)$.
$\text{C.}$ 当 $f^{\prime \prime}(x) \geq 0$ 时, $f(x) \geq g(x)$.
$\text{D.}$ 当 $f^{\prime \prime}(x) \geq 0$ 时, $f(x) \leq g(x)$.
设函数 $f_i(x)(i=1,2)$ 具有二阶连续导数, 且 $f_i^{\prime \prime}\left(x_0\right) < 0(i=1,2)$. 若两条曲线 $y=f_i(x)(i=1,2)$ 在点 $\left(x_0, y_0\right)$ 处具有公切线 $y=g(x)$, 且该点 处曲线 $y=f_1(x)$ 的曲率大于曲线 $y=f_2(x)$ 的曲率, 则在 $x_0$ 的某个邻域内 , 有
$\text{A.}$ $f_1(x) \leq f_2(x) \leq g(x)$.
$\text{B.}$ $f_2(x) \leq f_1(x) \leq g(x)$.
$\text{C.}$ $f_1(x) \leq g(x) \leq f_2(x)$.
$\text{D.}$ $f_2(x) \leq g(x) \leq f_1(x)$.
已知函数 $f(x)=\left\{\begin{array}{ll}2(x-1), & x < 1, \\ \ln x, & x \geq 1,\end{array}\right.$ 则 $f(x)$ 的一个原函数是
$\text{A.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1 \\ x(\ln x-1), & x \geq 1\end{cases}$
$\text{B.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1 \\ x(\ln x+1)-1, & x \geq 1\end{cases}$
$\text{C.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1, \\ x(\ln x+1)+1, & x \geq 1 .\end{cases}$
$\text{D.}$ $F(x)= \begin{cases}(x-1)^2, & x < 1, \\ x(\ln x-1)+1, & x \geq 1\end{cases}$
设函数 $f(x)$ 是连续函数, 则下列结论中正确的个数是
(1)若 $f(x)$ 在任意区间 $[a, b]$ 上满足 $\int_a^b f(x) \mathrm{d} x=0$, 则 $f(x) \equiv 0$.
(2)若 $f(x) \geq 0$, 并且存在区间 $[a, b]$ 使得 $\int_a^b f(x) \mathrm{d} x=0$, 则 $f(x)=0(x \in[a, b])$.
(3) 若 $\left[a_1, b_1\right] \subset[a, b]$, 则 $\int_{a_1}^{b_1} f(x) \mathrm{d} x \leq \int_a^b f(x) \mathrm{d} x$.
(4) 设 $g(x)$ 连续. 若 $f(x)>g(x), a, b$ 为不相等的常数, 则 $\int_a^b f(x) \mathrm{d} x>\int_a^b g(x) \mathrm{d} x$.
$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
设 $f(x)$ 是连续函数, 且 $F(x)=\int_x^{\mathrm{e}^{-x}} f(t) \mathrm{d} t$, 则 $F^{\prime}(x)$ 等于
$\text{A.}$ $-\mathrm{e}^{-x} f\left(\mathrm{e}^{-x}\right)-f(x)$.
$\text{B.}$ $-\mathrm{e}^{-x} f\left(\mathrm{e}^{-x}\right)+f(x)$.
$\text{C.}$ $\mathrm{e}^{-x} f\left(\mathrm{e}^{-x}\right)-f(x)$.
$\text{D.}$ $\mathrm{e}^{-x} f\left(\mathrm{e}^{-x}\right)+f(x)$.
$\lim _{n \rightarrow \infty} \sum_{i=1}^n \sum_{j=1}^n \frac{n}{(n+i)\left(n^2+j^2\right)}=$
$\text{A.}$ $\int_0^1 \mathrm{~d} x \int_0^x \frac{1}{(1+x)\left(1+y^2\right)} \mathrm{d} y$.
$\text{B.}$ $\int_0^1 \mathrm{~d} x \int_0^x \frac{1}{(1+x)(1+y)} \mathrm{d} y$.
$\text{C.}$ $\int_0^1 \mathrm{~d} x \int_0^1 \frac{1}{(1+x)(1+y)} \mathrm{d} y$.
$\text{D.}$ $\int_0^1 \mathrm{~d} x \int_0^1 \frac{1}{(1+x)\left(1+y^2\right)} \mathrm{d} y$.
设 $f(x, y)$ 在 $D=\left\{(x, y) \mid x^2+y^2 \leq a^2\right\}$ 上连续, 则 $\lim _{a \rightarrow 0} \frac{1}{a^2} \iint_D f(x, y) \mathrm{d} \sigma $
$\text{A.}$ 不一定存在.
$\text{B.}$ 存在且等于 $f(0,0)$.
$\text{C.}$ 存在且等于 $\pi f(0,0)$.
$\text{D.}$ 存在且等于 $\frac{1}{\pi} f(0,0)$.
设区域 $D=\{(x, y)|| x|+| y \mid \leq 1\} . D_1$ 是 $D$ 在第一象限内的部分. $f(x, y)$ 在 $D$ 上连续, 等式 $\iint_D f(x, y) \mathrm{d} x \mathrm{~d} y=4 \iint_{D_1} f(x, y) \mathrm{d} x \mathrm{~d} y$ 成立的充分条件是
$\text{A.}$ $f(-x,-y)=f(x, y)$.
$\text{B.}$ $f(-x,-y)=-f(x, y)$.
$\text{C.}$ $f(-x, y)=f(x,-y)=-f(x, y)$.
$\text{D.}$ $f(-x, y)=f(x,-y)=f(x, y)$.
如图, 正方形 $\{(x, y)|| x|\leq 1| y \mid, \leq 1\}$ 被其对角线划分为四个 区域 $D_k(k=1,2,3,4), I_k=\iint_{D_k} y \cos x \mathrm{~d} x \mathrm{~d} y$, 则 $\max _{1 \leq k \leq 4}\left\{I_k\right\}=$
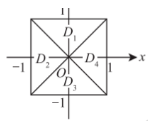
$\text{A.}$ $I_1$.
$\text{B.}$ $I_2$.
$\text{C.}$ $I_3$.
$\text{D.}$ $I_4$.
设区域 $D$ 由曲线 $y=\sin x, x= \pm \frac{\pi}{2}, y=1$ 围成, 则 $\iint_D\left(x y^5-1\right) \mathrm{d} x \mathrm{~d} y=$
$\text{A.}$ $\pi$.
$\text{B.}$ $2$.
$\text{C.}$ $-2$.
$\text{D.}$ $-\pi$.
设函数 $f(u)$ 连续, 区域 $D=\left\{(x, y) \mid x^2+y^2 \leq 2 y\right\}$, 则 $\iint_D f(x y) \mathrm{d} x \mathrm{~d} y$ 等于
$\text{A.}$ $\int_{-1}^1 \mathrm{~d} x \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} f(x y) \mathrm{d} y$
$\text{B.}$ $2 \int_0^2 \mathrm{~d} y \int_0^{\sqrt{2 y-y^2}} f(x y) \mathrm{d} x$.
$\text{C.}$ $\int_0^\pi \mathrm{d} \theta \int_0^{2 \sin \theta} f\left(r^2 \sin \theta \cos \theta\right) \mathrm{d} r$.
$\text{D.}$ $\int_0^\pi \mathrm{d} \theta \int_0^{2 \sin \theta} f\left(r^2 \sin \theta \cos \theta\right) r \mathrm{~d} r$.
下列计算极限的过程正确的是
$\text{A.}$ $\lim _{x \rightarrow+\infty}\left(\sqrt{x^2+1}-x\right)=\lim _{x \rightarrow+\infty} \sqrt{x^2+1}-\lim _{x \rightarrow+\infty} x=\infty-\infty=0$.
$\text{B.}$ $\lim _{x \rightarrow 0} x \sin \frac{1}{x}=\lim _{x \rightarrow 0} x \cdot \lim _{x \rightarrow 0} \sin \frac{1}{x}=0$.
$\text{C.}$ $\lim _{x \rightarrow+\infty} \frac{\sqrt{x}}{x}=\frac{\lim _{x \rightarrow+\infty} \sqrt{x}}{\lim _{x \rightarrow+\infty} x}=\frac{\infty}{\infty}=1$.
$\text{D.}$ $\lim _{x \rightarrow 0} \frac{x^2-x}{x^2+x}=\lim _{x \rightarrow 0} \frac{x(x-1)}{x(x+1)}=\lim _{x \rightarrow 0} \frac{x-1}{x+1}=\frac{\lim _{x \rightarrow 0}(x-1)}{\lim _{x \rightarrow 0}(x+1)}=\frac{-1}{1}=-1$.
若 $\lim _{x \rightarrow x_0} f(x)=\infty, \lim _{x \rightarrow x_0} g(x)=\infty$, 则
$\text{A.}$ $\lim _{x \rightarrow x_0}[f(x)+g(x)]=\infty$.
$\text{B.}$ $\lim _{x \rightarrow x_0}[f(x)-g(x)]=\infty$.
$\text{C.}$ $\lim _{x \rightarrow x_0} f(x) g(x)=\infty$.
$\text{D.}$ $\lim _{x \rightarrow x_0} \frac{f(x)}{g(x)}=\infty$.
设当 $x \rightarrow 0$ 时, $\mathrm{e}^x-\left(a x^2+b x+1\right)$ 是比 $x^2$ 高阶的无穷小, 则
$\text{A.}$ $a=\frac{1}{2}, b=1$.
$\text{B.}$ $a=1, b=1$.
$\text{C.}$ $a=-\frac{1}{2}, \quad b=-1$.
$\text{D.}$ $a=-1, b=1$.
$\lim _{x \rightarrow 0} \frac{a \tan x+b(1-\cos x)}{c \ln (1-2 x)+d\left(1-\mathrm{e}^{-x^2}\right)}=2$, 其中 $a^2+c^2 \neq 0$, 则必有
$\text{A.}$ $b=4 d$.
$\text{B.}$ $b=-4 d$.
$\text{C.}$ $a=4 c$.
$\text{D.}$ $a=-4 c$.
已知 $y=\frac{x}{\ln x}$ 是微分方程 $y^{\prime}=\frac{y}{x}+\varphi\left(\frac{x}{y}\right)$ 的解, 则 $\varphi\left(\frac{x}{y}\right)$ 的表达式为
$\text{A.}$ $-\frac{y^2}{x^2}$.
$\text{B.}$ $\frac{y^2}{x^2}$.
$\text{C.}$ $-\frac{x^2}{y^2}$.
$\text{D.}$ $\frac{x^2}{y^2}$.
已知级数 $\sum_{n=1}^{\infty}(-1)^{n-1} a_n=2, \sum_{n=1}^{\infty} a_{2 n-1}=5$, 则级数 $\sum_{n=1}^{\infty} a_n$ 等于
$\text{A.}$ 3
$\text{B.}$ 7
$\text{C.}$ 8
$\text{D.}$ 9
设 $u_n \neq 0(n=1,2,3, \cdots)$, 且 $\lim _{n \rightarrow \infty} \frac{n}{u_n}=1$, 则级数 $\sum_{n=1}^{\infty}(-1)^{n+1}\left(\frac{1}{u_n}+\frac{1}{u_{n+1}}\right)$
$\text{A.}$ 发散.
$\text{B.}$ 绝对收敛.
$\text{C.}$ 条件收敛.
$\text{D.}$ 收敛性根据所给条件不能判定.