单选题 （共 10 题 ），每题只有一个选项正确
若 $\frac{a}{b}=\frac{3}{2}$ ，则 $\frac{a+b}{b}=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{3}{2}$
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ $\frac{3}{5}$
抛物线 $y=a(x+1)^2+2(a \neq 0)$ 的对称轴是
$\text{A.}$ 直线 $x=1$
$\text{B.}$ 直线 $x=2$
$\text{C.}$ 直线 $x=-1$
$\text{D.}$ 直线 $x=-2$
若 $\triangle A B C \backsim \triangle D E F, \triangle A B C$ 与 $\triangle D E F$ 的周长比为 $1: 4$ ，则 $A B: D E=$
$\text{A.}$ $1: 2$
$\text{B.}$ $1 : 4$
$\text{C.}$ $1: 8$
$\text{D.}$ $1: 16$
若点 $(2,-3)$ 在反比例函数 $y=\frac{k}{x}(k \neq 0)$ 的图象上，则该图象也过点
$\text{A.}$ $(2,3)$
$\text{B.}$ $(3,2)$
$\text{C.}$ $(-2,-3)$
$\text{D.}$ $(-3,2)$
如图，直线 $l_1 / / l_2 / / l_3$ ，直线 $A C$ 分别交 $l_1, l_2, l_3$ 于点 $A, B, C$ ，直线 $D F$ 分别交 $l_1, l_2, l_3$ 于点 $D, E, F$ ，直线 $A C$ 与 $D F$ 相交于点 $G$ ．若 $A G=2, B G=1, B C=5$ ，则下列结论正确的是
$\text{A.}$ $\frac{E G}{D G}=\frac{2}{3}$
$\text{B.}$ $\frac{E G}{F G}=\frac{1}{6}$
$\text{C.}$ $\frac{E D}{E F}=\frac{1}{2}$
$\text{D.}$ $\frac{E B}{F C}=\frac{1}{5}$
如图，$\triangle O A B$ 与 $\triangle O C D$ 是以点 $O$ 为位似中心的位似图形，相似比为 $1: 2, \angle O A B=90^{\circ}$ ， $A O=A B$ ．若 $B(1,0)$ ，则点 $C$ 的坐标为
$\text{A.}$ $(1,2)$
$\text{B.}$ $(1,1)$
$\text{C.}$ $(\sqrt{2}, \sqrt{2})$
$\text{D.}$ $(2,1)$
若函数 $y=(a-3) x^2-4 x+2$ 的图象与 $x$ 轴只有一个交点，则 $a$ 的值是
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 3 或 5
若反比例函数 $y=\frac{2}{x}$ 的图象上有 $P\left(t, y_1\right), M\left(t+1, y_2\right), Q\left(t-1, y_3\right)$ 三点，则下列说法正确的是
$\text{A.}$ 当 $t < -1$ 时，$y_2 < y_1 < y_3 < 0$
$\text{B.}$ 当 $t < 0$ 且 $t \neq-1$ 时，$y_2 < y_1 < y_3 < 0$
$\text{C.}$ 当 $t>1$ 时， $0 < y_1 < y_2 < y_3$
$\text{D.}$ 当 $t>0$ 且 $t \neq 1$ 时， $0 < y_1 < y_2 < y_3$
在同一平面直角坐标系中，二次函数 $y=a x^2-b(a \neq 0)$ 和一次函数 $y=a x-b(a \neq 0)$ 的图象大致为
$\text{A.}$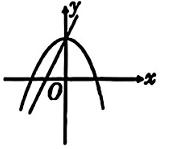 
$\text{B.}$ 
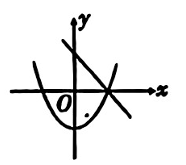$\text{C.}$ 
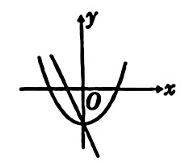$\text{D.}$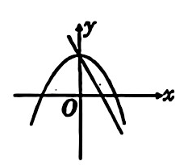 
如图，在正方形 $A B C D$ 中，$E$ 为 $A B$ 的中点，$F$ 是 $A D$ 边上的一个动点，连接 $E F$ ，将 $\triangle A E F$ 沿 $E F$ 折叠得到 $\triangle H E F$ ，延长 $F H$ 交 $B C$ 于点 $M$ ，连接 $E M$ ．下列结论错误的是
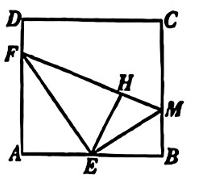
$\text{A.}$ $\triangle E F M$ 是直角三角形
$\text{B.}$ $\triangle B E M \cong \triangle H E M$
$\text{C.}$ 当点 $M$ 与点 $C$ 重合时，$D F=3 A F$
$\text{D.}$ $M F$ 平分正方形 $A B C D$ 的面积
填空题 （共 4 题 ），请把答案直接填写在答题纸上
已知二次函数 $y=2(x-1)^2$ ，当 $x>1$ 时，$y$ 随 $x$ 的增大而 $\_\_\_\_$ （填＂增大＂或＂減小＂）．
已知线段 $a=4$ ，线段 $b=9$ ，线段 $c$ 是线段 $a, b$ 的比例中项，则线段 $c$ 的长为
如图，在等边三角形 $A B C$ 中，点 $D, E$ 分别在边 $B C, A B$ 上，$\angle A D E=60^{\circ}$ ．若 $B D=4 D C$ ， $D E=2.4$ ，则 $A D$ 的长为
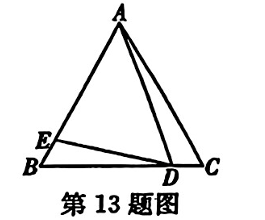
如图，在平面直角坐标系中，点 $Q$ 在 $y$ 轴正半轴上，点 $R$ 在 $x$ 轴正半轴上，以 $O R$ 为边向上作等边 $\triangle O R S, O S$ 交 $R Q$ 于点 $T$ ，反比例函数 $y=\frac{k}{x}(k \neq 0)$ 的图象交 $R Q$ 于点 $T, U$ ．若 $T U : R Q=1: 3, \triangle O Q T$ 的面积为 $\sqrt{3}$ ．
（1）$k$ 的值为 $\_\_\_\_$ ；
（2）$\triangle O S R$ 的面积为 $\_\_\_\_$ ．
解答题 （共 9 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
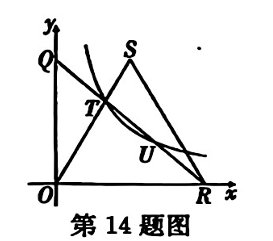
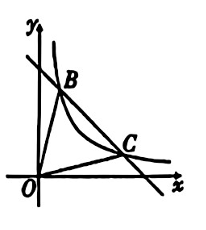
已知蓄电池的电压为定值，使用某蓄电池时，电流 $I$（单位： A ）与电阻 $R$ （单位：$\Omega$ ）是反比例函数关系，它的图象如图所示，当电阻 $R$ 为 $4 \Omega$ 时，求电流 $I$
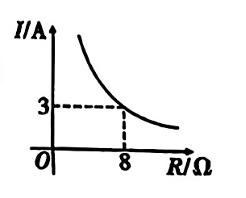
如图，在平面直角坐标系中，$\triangle A B C$ 的顶点坐标分别为 $A(3,1)$ ， $B(1,2), C(4,3)$ ．
（1）以原点 $O$ 为位似中心，在第一象限内画出 $\triangle A B C$ 的位似图形 $\triangle A_1 B_1 C_1$ ，使 $\triangle A_1 B_1 C_1$ 与 $\triangle A B C$ 的相似比为 $2: 1$ ；
（2）写出点 $A_1$ 的坐标．
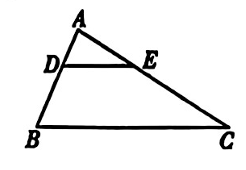
如图，在 $\triangle A B C$ 中，$D E / / B C, A E=B D$ ．若 $A B=6, A C=10$ ，求 $A E$ 的长．
已知二次函数 $y=a x^2+b x+c(a \neq 0)$ 的 $y$ 与 $x$ 的部分对应值如表：
（1）求该二次函数的表达式；
（2）在如图所示的平面直角坐标系中画出该二次函数的图象；
（3）当 $y>-3$ 时，$x$ 的取值范围为 $\_\_\_\_$
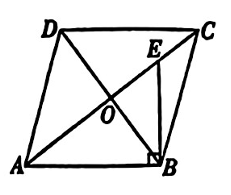
如图，在 $\square A B C D$ 中，对角线 $A C, B D$ 相交于点 $O, \angle C A B=\angle A C B$ ，过点 $B$ 作 $B E \perp A B$ 交 $A C$ 于点 $E$ ．
（1）求证：$\triangle A B O \backsim \triangle B E O$ ；
（2）若 $A B=10, A C=16$ ，求 $C E$ 的长．
如图，反比例函数 $y=\frac{m}{x}(m \neq 0, x>0)$ 的图象与一次函数 $y=k x+6(k \neq 0)$ 的图象交于点 $B(1,5), C(n, 1)$.
（1）求 $m$ 和 $k$ 的值；
（2）求点 $C$ 的坐标，并根据图象直接写出关于 $x$ 的不等式 $\frac{m}{x} \leqslant k x+6(x> 0)$ 的解集；
（3）连接 $O B, O C$ ，求 $\triangle B O C$ 的面积．
某汽车研发中心设计了一款新型汽车，现在模拟汽车在高速公路上以某一速度行驶时，对它的刹车性能进行测试。研发小组成员记录其中一组数据如下：
发现： ① 开始刹车后行驶的距离 $y$（单位：m）与刹车后行驶的时间 $t$（单位： s ）之间成二次函数关系；
② 汽车刹车后行驶的距离随刹车后行驶的时间 $t$ 的增大而增大，当刹车后行驶的距离最远时，汽车完全停止。
请根据以上信息，完成下列问题：
（1）求 $y$ 关于 $t$ 的函数表达式（不要求写出自变量的取值范囲）；
（2）求汽车刹车 4 s 后，行驶了多远距离；
（3）若驾驶员发现正前方 80 m 处有一辆抛针的车停在路面，立刻刹车，问该车在不变道的情况下是否会撞到拋锚的车？试说明理由．
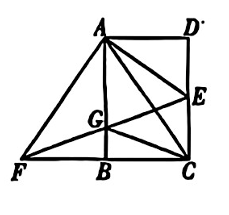
如图，在矩形 $A B C D$ 中，点 $E$ 是边 $C D$ 上任意一点（点 $E$ 与点 $C, D$ 不重合），过点 $A$ 作 $A F \perp A E$ ，交边 $C B$ 的延长线于点 $F$ ，连接 $E F$ 交边 $A B$ 于点 $G$ ，连接 $A C$ ．
（1）求证：$\triangle A E F \backsim \triangle D A C$ ；
（2）若 $F E$ 平分 $\angle A F B$ ，连接 $C G$ ，求证：四边形 $A G C E$ 为菱形．
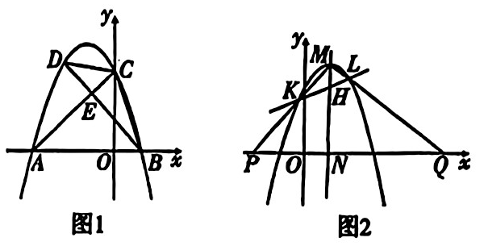
已知抛物线 $C_1: y=-x^2-2 x+3$ 与 $x$ 轴相交于 $A, B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴相交于点 $C$ ，连接 $A C$ ．
（1）求直线 $A C$ 的表达式；
（2）如图 1 ，点 $D$ 在第二象限内抛物线 $C_1$ 上，连接 $B D$ 交 $A C$ 于点 $E$ ，连接 $B C$ ．若 $S_{\triangle C B E}= 2 S_{\triangle C D E}$ ，求点 $D$ 的坐标；
（3）如图 2，将抛物线 $C_1$ 向右平移 2 个单位长度，得到抛物线 $C_2$ ，过拋物线 $C_2$ 的顶点 $M$ 作 $M N \perp x$ 轴，垂足为点 $N$ ，过线段 $M N$ 上的点 $H$ 的直线与抛物线 $C_2$ 交于 $K, L$ 两点，直线 $M K, M L$ 分别与 $x$ 轴交于 $P, Q$ 两点．若 $N P \cdot N Q=16$ ，求点 $H$ 的坐标．
