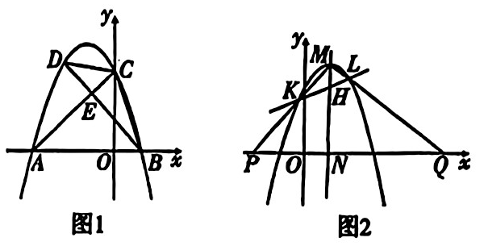
已知抛物线 $C_1: y=-x^2-2 x+3$ 与 $x$ 轴相交于 $A, B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴相交于点 $C$ ，连接 $A C$ ．
（1）求直线 $A C$ 的表达式；
（2）如图 1 ，点 $D$ 在第二象限内抛物线 $C_1$ 上，连接 $B D$ 交 $A C$ 于点 $E$ ，连接 $B C$ ．若 $S_{\triangle C B E}= 2 S_{\triangle C D E}$ ，求点 $D$ 的坐标；
（3）如图 2，将抛物线 $C_1$ 向右平移 2 个单位长度，得到抛物线 $C_2$ ，过拋物线 $C_2$ 的顶点 $M$ 作 $M N \perp x$ 轴，垂足为点 $N$ ，过线段 $M N$ 上的点 $H$ 的直线与抛物线 $C_2$ 交于 $K, L$ 两点，直线 $M K, M L$ 分别与 $x$ 轴交于 $P, Q$ 两点．若 $N P \cdot N Q=16$ ，求点 $H$ 的坐标．