单选题 (共 9 题 ),每题只有一个选项正确
在随机事件 $A, B, C$ 中,$A$ 和 $B$ 两事件至少有一个发生而 $C$ 事件不发生的随机事件可表示为
$\text{A.}$ $\mathrm{A} \overline{\mathrm{C}} \cup \mathrm{B} \overline{\mathrm{C}}$
$\text{B.}$ $\mathrm{AB} \overline{\mathrm{C}}$
$\text{C.}$ $\mathrm{AB} \overline{\mathrm{C}} \cup \mathrm{A} \overline{\mathrm{B}} \mathrm{C} \cup \overline{\mathrm{A}} \mathrm{B} \mathrm{C}$
$\text{D.}$ $\mathrm{A} \cup \mathrm{B} \cup \overline{\mathrm{C}}$
袋中有 5 个黑球, 3 个白球,大小相同,一次随机地摸出 4 个球,其中恰有 3 个白球的概率为
$\text{A.}$ $\frac{3}{8}$
$\text{B.}$ $\left(\frac{3}{8}\right)^5 \frac{1}{8}$
$\text{C.}$ $\mathrm{C}_8^4\left(\frac{3}{8}\right)^3 \frac{1}{8}$
$\text{D.}$ $\frac{5}{\mathrm{C}_8^4}$
设 A 、 B 互为对立事件,且 $P(A)>0, P(B)>0$ ,则下列各式中错误的是
$\text{A.}$ $P(\bar{B} \mid A)=0$
$\text{B.}$ $P(A \mid B)=0$
$\text{C.}$ $P(A B)=0$
$\text{D.}$ $P(A \cup B)=1$
离散型随机变量 X 的分布列为 $\mathrm{P}\{X=k\}=a k, k=1,2,3,4$ .则 $a=(\quad)$
$\text{A.}$ 0.05
$\text{B.}$ 0.1
$\text{C.}$ 0.2
$\text{D.}$ 0.25
设随机变量 X 的分布函数为 $F(x)=a+\frac{1}{\pi} \arctan x(-\infty < x < \infty, a$ 为常数 $)$ 则
$$
P\left\{-\frac{\sqrt{3}}{3} < X < \sqrt{3}\right\}=
$$
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{3}$
设随机变量 X 服从 $N(\mu, 4)$ ,则 $P\{X \leq 2+\mu\}$ ,的值
$\text{A.}$ 随 $\mu$ 增大而减小;
$\text{B.}$ 随 $\mu$ 增大而增大;
$\text{C.}$ 随 $\mu$ 增大而不变;
$\text{D.}$ 随 $\mu$ 减少而增大.
设随机变量 $X \sim N\left(\mu, \sigma^2\right)$ ,则 $Y=a X+b$ 服从
$\text{A.}$ $N\left(\mu, \sigma^2\right)$
$\text{B.}$ $N(0,1)$
$\text{C.}$ $N\left(\frac{\mu}{a},\left(\frac{\sigma}{b}\right)^2\right)$
$\text{D.}$ $N\left(a \mu+b, a^2 \sigma^2\right)$
对目标进行 3 次独立射击,每次射击的命中率相同,如果击中次数的方差为 0.72 ,则每次射击的命中率等于
$\text{A.}$ 0.1
$\text{B.}$ 0.2
$\text{C.}$ 0.3
$\text{D.}$ 0.4
设随机变量 X 的概率密度为 $f(x)=\left\{\begin{array}{cl}\frac{1}{\pi \sqrt{a^2-x^2}} & |x| < a \\ 0 & |x| \geq a\end{array}, a>0\right.$ ,则 $E(X)=$
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ 1
$\text{D.}$ 以上结论均不正确
填空题 (共 11 题 ),请把答案直接填写在答题纸上
$A 、 B 、 C$ 代表三事件,事件"$A 、 B 、 C$ 至少有二个发生"可表示为
事件 A、B 相互独立,且知 $P(A)=0.2, P(B)=0.5$ 则 $P(A \cup B)=$
若随机事件 $A$ 和 $B$ 都不发生的概率为 $p$ ,则 $A$ 和 $B$ 至少有一个发生的概率为
在相同条件下,对目标独立地进行 5 次射击,如果每次射击命中率为 0.6 ,那么击中目标 k 次的概率为
设随机变量 X 服从泊松分布,且 $\mathrm{P}\{X=1\}=\mathrm{P}\{X=2\}$ ,则 $\mathrm{P}\{X=3\}=$
设随机变量 X 的分布密度为 $f(x)=\left\{\begin{array}{rl}x & 0 \leq x < 1 \\ a-x & 1 \leq x < 2 \\ 0 & \text { 其它 }\end{array}\right.$ ,则 $a=$
若二维随机变量(X,Y)的联合分布律为
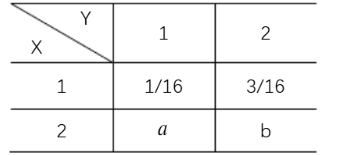
且 $\mathrm{X}, \mathrm{Y}$ 相互独立,则常数 $a=$ $\_\_\_\_$ , $\mathrm{b}=$ $\_\_\_\_$
设 $X$ 的分布密度为 $f(x)$ ,则 $Y=X^3$ 的分布密度为
二维随机变量(X,Y)的联合分布律为
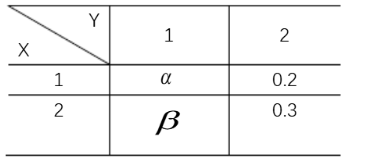
则 $\alpha$ 与 $\beta$ 应满足的条件是 $\_\_\_\_$ ,当 $\mathrm{X}, \mathrm{Y}$ 相互独立时,$\alpha=$
设随机变量 X 与 Y 相互独立,且 $X \sim N(1,2), Y \sim N(0,1)$ .令 $\mathrm{Z}=-\mathrm{Y}+2 \mathrm{X}+3$ ,则 $D(Z) =$ $\_\_\_\_$
已知随机变量 X 的数学期望 $E(X)=1, E\left(X^2\right)=4$ 。令 $Y=2 X-3$ ,则 $D(Y) =$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某工人看管甲、乙、丙 3 台机器,在 1 小时内,这 3 台机器不需照管的概率分别为 $0.8 ,0.9,0.6$ ,设这三台机器是否需照管是相互独立的,求在 1 小时内
(1)有机床需要工人照管的概率;(2)机床因无人照管而停工的概率.
设随机变量 X 的分布密度为 $f(x)=\frac{A}{1+x^2} \quad(-\infty < x < +\infty)$
求(1)常数 $A$ ;(2)$X$ 的分布函数;
设二维随机变量 $(\mathrm{X}, \mathrm{Y})$ 在区域 $0 \leq x \leq 1, y^2 \leq x$ 内服从均匀分布.求
(1)$(X, Y)$ 的联合分布密度;
(2)$X$ 与 $Y$ 的边缘分布密度,并问它们是否相互独立?
设 $\mathrm{X}, \mathrm{Y}$ 是两个相互独立的随机变量,其概率密度分别为
$$
f_X(x)=\left\{\begin{array}{cc}
1, & 0 \leq x \leq 1 \\
0, & \text { 其它 }
\end{array} \quad f_Y(y)=\left\{\begin{array}{c}
e^{-y}, y>0 \\
0, y \leq 0
\end{array}\right.\right.
$$
求随机变量 $Z=X+Y$ 的概率密度函数.
一工厂生产的某种设备的寿命 $\times$(以年计)服从指数分布,密度函数为
$$
f(x)=\left\{\begin{array}{cc}
\frac{1}{4} e^{-\frac{1}{4} x} & 0 < x \\
0 & x \leq 0
\end{array}\right.
$$
为确保消费者的利益,工厂规定出售的设备若在一年内损坏可以调换,若售出一台设备,工厂获利 100 元,而调换一台则损失 200 元.求工厂出售一台设备赢利的数学期望.
设随机变量( $\mathrm{X}, \mathrm{Y}$ )服从正态分布,且 X 和 Y 分别服从正态分布 $N\left(1,3^2\right)$
和 $N\left(0,4^2\right)$ , X 与 Y 的相关系数 $\rho_{X Y}=-\frac{1}{2}, Z=\frac{X}{3}+\frac{Y}{2}$ ,求 Z 的数学期望 $E(Z)$ 和方差 $D(Z)$ ;