单选题 (共 8 题 ),每题只有一个选项正确
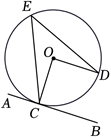
如图,$A B 、 C D$ 是 $\odot O$ 的两条直径,点 $E$ 是弧 $B D$ 的中点,连接 $A C 、 B E$ ,若 $\angle A C D=20^{\circ}$ ,则 $\angle A B E$ 的度数
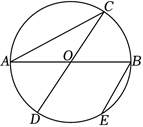
$\text{A.}$ $40^{\circ}$
$\text{B.}$ $44^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $55^{\circ}$
如图 $A, B, C$ 是 $\odot O$ 上的三点,$\angle A O B=60^{\circ}$ ,则 $\angle A C B$ 的度数是
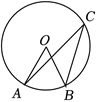
$\text{A.}$ $40^{\circ}$
$\text{B.}$ $35^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $25^{\circ}$
如图,$A B$ 是 $\odot O$ 的直径,$C, D$ 为 $\odot O$ 上两点,若 $A B=6, A C=3$ ,则 $\angle A D C$ 的度数是( )
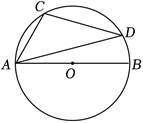
$\text{A.}$ $15^{\circ}$
$\text{B.}$ $30^{\circ}$
$\text{C.}$ $45^{\circ}$
$\text{D.}$ $60^{\circ}$
如图,$A B$ 是 $\odot O$ 的弦,$O C \perp A B$ 交 $\odot O$ 于点 $C$ ,点 $D$ 是优弧 $A B$ 上一点,若 $\angle A O C=37^{\circ}$ ,则 $\angle C D B=$( )
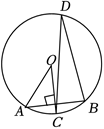
$\text{A.}$ $18.5^{\circ}$
$\text{B.}$ $37^{\circ}$
$\text{C.}$ $53^{\circ}$
$\text{D.}$ $74^{\circ}$
如图,直线 $A B$ 与 $\odot O$ 相切于点 $A, C D$ 是 $\odot O$ 的一条弦,且 $C D / / A B$ ,连接 $A C$ .若 $\odot O$ 的半径为 $2, C D=2 \sqrt{3}$ ,则阴影部分的面积为
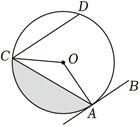
$\text{A.}$ $\frac{4 \pi}{3}-\sqrt{3}$
$\text{B.}$ $4 \pi$
$\text{C.}$ $4 \sqrt{2} \pi-\sqrt{3}$
$\text{D.}$ $\frac{2}{3} \pi-\frac{\sqrt{3}}{3}$
若一个正三角形和一个正六边形的面积相等,则正三角形与正六边形的边长比为
$\text{A.}$ $\sqrt{6}: 1$
$\text{B.}$ $1: \sqrt{6}$
$\text{C.}$ $\sqrt{3}: 1$
$\text{D.}$ $2: 1$
如图,四边形 $A B C D$ 内接于 $\odot O$ ,连接 $O B, O D, B D$ ,若 $\angle C=105^{\circ}$ ,则 $\angle O B D$ 的度数为
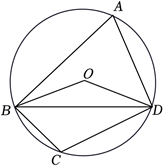
$\text{A.}$ $15^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $25^{\circ}$
$\text{D.}$ $30^{\circ}$
已知正多边形的一个外角为 $72^{\circ}$ ,则该正多边形的边数是
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ 8
$\text{D.}$ 10
填空题 (共 8 题 ),请把答案直接填写在答题纸上
如图,$P A, P B$ 与 $\odot O$ 分别相切于点 $A, B, P A=2, \angle P=60^{\circ}$ ,则 $A B=$
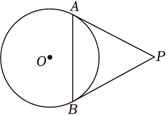
如图,直线 $A B$ 是 $\odot O$ 的切线,$C$ 为切点,$O D / / A B$ 交 $\odot O$ 于点 $D$ ,点 $E$ 在 $\odot O$ 上,连接 $O C$ , $E C, E D$ ,则 $\angle C E D$ 的度数为
一个圆锥的底面直径是 8 cm ,母线长为 9 cm ,则该圆锥的侧面积为 (结果保留 $\pi$ ).
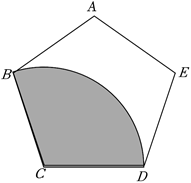
如图,从一个边长是 $a$ 的正五边形纸片上剪出一个扇形,这个扇形的面积为 (用含 $\pi$ 的代数式表示).
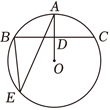
如图,$\odot O$ 的半径 $O A$ 与弦 $B C$ 互相平分,则 $\angle A E B$ 的度数为
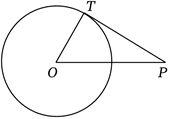
如图,点 $P$ 是 $\odot O$ 外一点,$P T$ 是 $\odot O$ 的切线,$T$ 为切点,连接 $O T$ .若 $\angle P=35^{\circ}$ ,则 $\angle O$
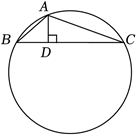
如图,$\odot O$ 的直径为 $m, \triangle A B C$ 是 $\odot O$ 的内接三角形,$A B$ 的长为 $x, A C$ 的长为 $y$ ,且 $x+y =6, A D \perp B C$ 于点 $D, A D=1$ ,则 $m$ 的最大值为
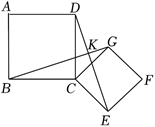
如图,正方形 $A B C D$ 的边长为 6 ,正方形 $C E F G$ 的边长为 $3 \sqrt{2}$ ,将正方形 $C E F G$ 绕点 $C$ 旋转,$B G$ 和 $D E$ 相交于点 $K$ ,则 $A K$ 的最大值是 .连结 $B E$ ,当点 $C$ 正好是 $\triangle B K E$的内心时,$C K$ 的长是
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
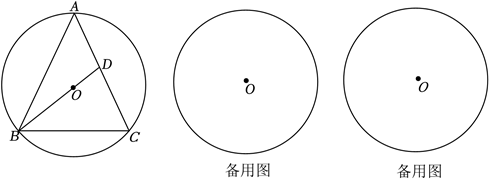
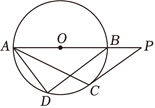
如图,$\odot O$ 是 $\triangle A B D$ 的外接圆,$A B$ 是 $\odot O$ 的直径,点 $C$ 在 $\odot O$ 上,连接 $A C$ ,且 $A C$ 平分 $\angle D A B$ ,过点 $C$ 作 $\odot O$ 的切线交 $A B$ 的延长线于点 $P$ .
(1)求证:$B D / / C P$ ;
(2)若 $\cos P=\frac{4}{5}, B D=24$ ,求 $B P$ 的长.
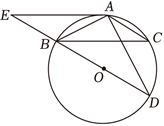
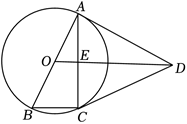
如图,$B D$ 为 $\odot O$ 直径,点 $A 、 C$ 在 $\odot O$ 上,$\angle B A C=120^{\circ}, A B=A C$ ,点 $E$ 为 $D B$ 延长线上一点,$\angle B E A=30^{\circ}$ .
(1)求证:$A E$ 为 $\odot O$ 的切线;
(2)判断四边形 $A E B C$ 的形状并说明理由.
如图,四边形 $A B C D$ 中,$A B=A D=C D$ ,以 $A B$ 为直径的 $\odot O$ 经过点 $C$ ,连接 $A C 、 O D$ 交于点 $E$ .
(1)证明:$O D / / B C$ ;
(2)若 $\tan \angle A B C=2$ ,证明:$D A$ 与 $\odot O$ 相切.
如图,锐角 $\triangle A B C$ 中,$A B=A C, \odot O$ 是 $\triangle A B C$ 的外接圆,$B O$ 的延长线交边 $A C$ 于点 $D$ .
(1)求证:$\angle B A C=2 \angle A B D$ ;
(2)当 $\triangle B C D$ 是等腰三角形时,求 $\angle A B D$ 的度数;
(3)记 $\triangle A B C 、 \triangle A B D 、 \triangle B C D$ 的面积分别为 $S 、 S_1 、 S_2$ ,且 $\frac{1}{S}+\frac{1}{S_2}=\frac{1}{S_1}$ ,
① 求 $\frac{\mathrm{AD}}{\mathrm{CD}}$ 的值;
② 求 $\cos \angle B A C$ .