单选题 (共 12 题 ),每题只有一个选项正确
已知集合 $\mathrm{A}=\{x \in R|| x \mid \leqslant 2\}\}, B=\{x \in Z \mid \sqrt{x} \leqslant 4\}$, 则 $A \cap B=($ )
$\text{A.}$ $(0,2)$
$\text{B.}$ $[0,2]$
$\text{C.}$ $\{0,2\}$
$\text{D.}$ $\{0,1,2\}$
已知复数 $\mathrm{z}=\frac{\sqrt{3}+i}{(1-\sqrt{3} i)^{2}}, \bar{z}$ 是 $z$ 的共轭复数, 则 $z=\bar{z}=(\quad)$
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ 1
$\text{D.}$ 2
曲线 $\mathrm{y}=\frac{\mathrm{x}}{\mathrm{x}+2}$ 在点 $(-1,-1$ ) 处的切线方程为()
$\text{A.}$ $y=2 x+1$
$\text{B.}$ $y=2 x-1$
$\text{C.}$ $y=-2 x-3$
$\text{D.}$ $y=-2 x-2$
已知命题 $\mathrm{p}_{1}$ :函数 $\mathrm{y}=2^{\mathrm{x}}-2^{-\mathrm{x}}$ 在 $\mathrm{R}$ 为增函数, $\mathrm{p}_{2}$ : 函数 $\mathrm{y}=2^{\mathrm{x}}+2^{-\mathrm{x}}$ 在 $\mathrm{R}$ 为减函数, 则在命题 $\mathrm{q}_{1}: \mathrm{p}_{1} \vee \mathrm{p}_{2}, \mathrm{q}_{2}: \mathrm{p}_{1} \wedge \mathrm{p}_{2}, \mathrm{q}_{3}:\left(\neg \mathrm{p}_{1}\right) \vee \mathrm{p}_{2}$ 和 $\mathrm{q}_{4}: \mathrm{p}_{1} \wedge(\neg$ $\mathrm{p}_{2}$ )中, 真命题是()
$\text{A.}$ $\mathrm{q}_{1}, \mathrm{q}_{3}$
$\text{B.}$ $\mathrm{q}_{2}, \mathrm{q}_{3}$
$\text{C.}$ $\mathrm{q}_{1}, \mathrm{q}_{4}$
$\text{D.}$ $\mathrm{q}_{2}, \mathrm{q}_{4}$
某种种子每粒发芽的概率都为 $0.9$, 现播种了 1000 粒, 对于没有发 芽的种子, 每粒需再补种 2 粒, 补种的种子数记为 $X$, 则 $X$ 的数学期望为 ( )
$\text{A.}$ 100
$\text{B.}$ 200
$\text{C.}$ 300
$\text{D.}$ 400
如果执行如图的框图,输入 N=5,则输出的数等于( )
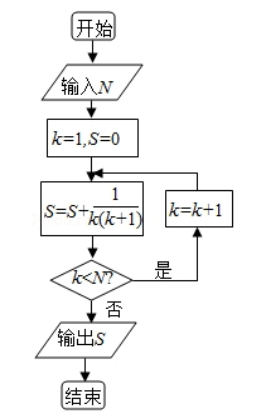
$\text{A.}$ $\frac{5}{4}$
$\text{B.}$ $\frac{4}{5}$
$\text{C.}$ $\frac{6}{5}$
$\text{D.}$ $\frac{5}{6}$
设偶函数 $f(x)$ 满足 $f(x)=2^{x}-4(x \geqslant 0)$ ,则 $\{x \mid f(x-2)>0\}=$ ( )
$\text{A.}$ $\{x \mid x < -2$ 或 $x>4\}$
$\text{B.}$ $\{x \mid x < 0$ 或 $x>4\}$
$\text{C.}$ $\{x \mid x < 0$ 或 $x>6\}$
$\text{D.}$ $\{x \mid x < -2$ 或 $x>2\}$
若 $\cos \alpha=-\frac{4}{5}, \alpha$ 是第三象限的角, 则 $\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}=$ ( )
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $2$
$\text{D.}$ $-2$
设三棱柱的侧棱垂直于底面, 所有棱长都为 $a$, 顶点都在一个球面 上, 则该球的表面积为 ( )
$\text{A.}$ $\pi a^{2}$
$\text{B.}$ $\frac{7}{3} \pi a^{2}$
$\text{C.}$ $\frac{11}{3} \pi a^{2}$
$\text{D.}$ $5 \pi a^{2}$
已知函数 $f(x)=\left\{\begin{array}{l}|\operatorname{lgx}|, \quad 0 < x \leqslant 10 \\ -\frac{1}{2} x+6, x>10\end{array}\right.$, 若 $a, b, c$ 互不相等, 且 $f(a)$ $=f(b)=f(c)$, 则 $a b c$ 的取值范围是 ( )
$\text{A.}$ $(1,10)$
$\text{B.}$ $(5,6)$
$\text{C.}$ $(10,12)$
$\text{D.}$ $(20,24)$
已知双曲线 $E$ 的中心为原点, $P(3,0)$ 是 $E$ 的焦点, 过 $P$ 的直线$I$ 与 $E$ 相交于 $A, B$ 两点, 且 $A B$ 的中点为 $N(-12,-15)$, 则 $E$ 的方程式为( )
$\text{A.}$ $\frac{x^{2}}{3}-\frac{y^{2}}{6}=1$
$\text{B.}$ $\frac{x^{2}}{4}-\frac{y^{2}}{5}=1$
$\text{C.}$ $\frac{x^{2}}{6}-\frac{y^{2}}{3}=1$
$\text{D.}$ $\frac{x^{2}}{5}-\frac{y^{2}}{4}=1$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
设 $\mathrm{y}=\mathrm{f}(\mathrm{x})$ 为区间 $[0,1]$ 上的连续函数, 且恒有 $0 \leqslant \mathrm{f}(\mathrm{x}) \leqslant 1$, 可 以用随机模拟方法近似计算积分 $\int_{0}^{1} \mathrm{f}(\mathrm{x}) \mathrm{dx}$, 先产生两组 (每组 $\mathrm{N}$ 个) 区间 [0, 1] 上的均匀随机数 $x_{1}, x_{2}, \ldots x_{N}$ 和 $y_{1}, y_{2}, \ldots y_{N}$, 由此得到 $N$ 个点 $\left(x_{i}, y_{i}\right)$ ( $i=1,2, \ldots, N)$, 再数出其中满足 $y_{i} \leqslant f\left(x_{i}\right) \quad(i=1,2, \ldots, N)$ 的点数 $N_{1}$, 那么由随机模拟方案可得积分 $\int_{0}^{1} f(x) d x$ 的近似值为( )
过点 $A(4,1)$ 的圆 $C$ 与直线 $x-y=1$ 相切于点 $B(2,1)$, 则圆 $C$ 的方程为 ( )
在 $\triangle A B C$ 中, $D$ 为边 $B C$ 上一点, $B D=\frac{1}{2} D C, \angle A D B=120^{\circ}, A D=2$, 若 $\triangle$ $A D C$ 的面积为 $3-\sqrt{3}$, 则 $\angle B A C=$ ( )
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设数列满足 $a_{1}=2, a_{n+1}-a_{n}=3 \cdot 2^{2 n-1}$
(1)求数列 $\left\{a_{n}\right\}$ 的通项公式;
(2) 令 $b_{n}=n a_{n}$, 求数列 $\left\{b_{n}\right\}$ 的前 $n$ 项和 $S_{n}$.
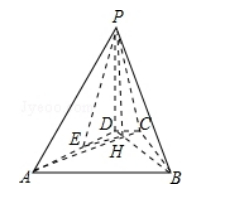
如图, 已知四棱雉 $P-A B C D$ 的底面为等腰梯形, $A B / / C D, A C \perp B D$
, 垂足为 $\mathrm{H}, \mathrm{PH}$ 是四棱雉的高, $\mathrm{E}$ 为 $\mathrm{AD}$ 中点
(I ) 证明: $P E \perp B C$
(II ) 若 $\angle \mathrm{APB}=\angle \mathrm{ADB}=60^{\circ}$, 求直线 $P A$ 与平面 $\mathrm{PEH}$ 所成角的正弦值.
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样
方法从该地区调查了 500 位老年人,结果如表:
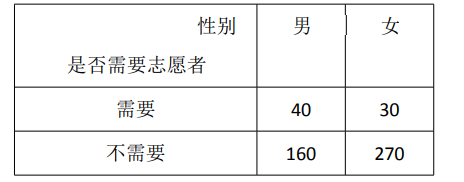
(1)估计该地区老年人中,需要志愿者提供帮助的比例;
(2)能否有 99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有
关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要
志愿者提供帮助的老年人比例?说明理由.

设 $F_{1}, F_{2}$ 分别是椭圆 $E: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的左、右焦点, 过 $F_{1}$ 斜率为 1 的直线 $\ell$ 与 $E$ 相交于 $A, B$ 两点, 且 $\left|A F_{2}\right|,|A B|,\left|B_{2}\right|$ 成等差数列
(1) 求 $\mathrm{E}$ 的离心率;
(2) 设点 $P(0,-1)$ 满足 $|P A|=|P B|$, 求 $E$ 的方程.
设函数 $f(x)=e^{x}-1-x^{-} a x^{2}$.
(1)若 $a=0$, 求 $f(x)$ 的单调区间;
(2)若当 $x \geqslant 0$ 时 $f(x) \geqslant 0$, 求 $a$ 的取值范围.
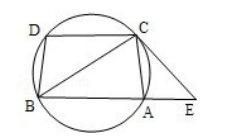
如图: 已知圆上的弧 $\widehat{A C}=\widehat{B D}$, 过 $C$ 点的圆的切线与 $B A$ 的延长线交
于 $E$ 点, 证明:
(I) $\angle \mathrm{ACE}=\angle \mathrm{BCD}$.
(II ) $\mathrm{BC}^{2}=\mathrm{BE} \cdot \mathrm{CD}$.
已知直线 $C_{1}\left\{\begin{array}{l}x=1+t \cos \alpha \\ y=t \sin \alpha\end{array}\right.$ (t 为参数) , $C_{2}\left\{\begin{array}{l}x=\cos \theta \\ y=\sin \theta\end{array}\right.$ ( $\theta$ 为参数),
(I)当 $\alpha=\frac{\pi}{3}$ 时, 求 $C_{1}$ 与 $C_{2}$ 的交点坐标;
(II) 过坐标原点 $O$ 做 $C_{1}$ 的垂线, 垂足为 $A, P$ 为 $O A$ 中点, 当 $\alpha$ 变化时, 求 $P$ 点的轨迹的参数方程, 并指出它是什么曲线.
设函数 $f(x)=|2 x-4|+1$.
(I) 画出函数 $\mathrm{y}=\mathrm{f}(\mathrm{x})$ 的图象:
(II) 若不等式 $f(x) \leqslant a x$ 的解集非空, 求 $a$ 的取值范围.