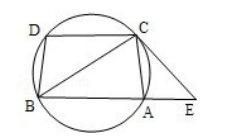
如图: 已知圆上的弧 $\widehat{A C}=\widehat{B D}$, 过 $C$ 点的圆的切线与 $B A$ 的延长线交
于 $E$ 点, 证明:
(I) $\angle \mathrm{ACE}=\angle \mathrm{BCD}$.
(II ) $\mathrm{BC}^{2}=\mathrm{BE} \cdot \mathrm{CD}$.
于 $E$ 点, 证明:
(I) $\angle \mathrm{ACE}=\angle \mathrm{BCD}$.
(II ) $\mathrm{BC}^{2}=\mathrm{BE} \cdot \mathrm{CD}$.
