单选题 (共 8 题 ),每题只有一个选项正确
甲、乙、丙、丁四名教师带领学生参加校园植树活动,教师随机分成三组,每组至少一人,则甲、乙在同一组的概率为
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{2}$
二项式 $\left(\sqrt{x}-\frac{2}{\sqrt[3]{x}}\right)^{5}$ 的展开式中常数项为
$\text{A.}$ 80
$\text{B.}$ -80
$\text{C.}$ -40
$\text{D.}$ 40
将 5 名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶 4 个项目进行培训,每名志愿者只分配到 1 个项目,每个项目至少分配 1 名志愿者,则不同的分配方案共有
$\text{A.}$ 60 种
$\text{B.}$ 120 种
$\text{C.}$ 240 种
$\text{D.}$ 480 种
已知随机变量 $X$ 服从正态分布 $N\left(4, \sigma^{2}\right)$ ,且 $P(3 \leq X \leq 5)=0.86$ ,则 $P(X < 3)=$
$\text{A.}$ . 0.43
$\text{B.}$ . 0.28
$\text{C.}$ . 0.14
$\text{D.}$ 0.07
假设有两箱零件,第一箱内装有 5 件,其中有 2 件次品;第二箱内装有 10 件,其中有 3 件次品.现从两箱中随机挑选 1 箱,然后从该箱中随机取 1 个零件,若取到的是次品,则这件次品是从第一箱中取出的概率为( )
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{3}{7}$
$\text{C.}$ $\frac{7}{20}$
$\text{D.}$ $\frac{4}{7}$
若多项式 $x^{2}+x^{10}=a_{0}+a_{1}(x+1)+\mathrm{L}+a_{9}(x+1)^{9}+a_{10}(x+1)^{10}$ ,则 $a_{3}=$
$\text{A.}$ 56
$\text{B.}$ -120
$\text{C.}$ -56
$\text{D.}$ 120
已知随机变量 $\xi_{i}$ 的分布列如下:
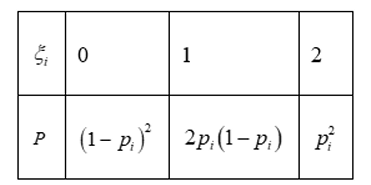
其中 $i=1,2$ ,若 $\frac{1}{2} < p_{1} < p_{2} < 1$ ,则
$\text{A.}$ $E\left(\xi_{1}\right) < E\left(\xi_{2}\right), \quad D\left(3 \xi_{1}+1\right) < D\left(3 \xi_{2}+1\right)$
$\text{B.}$ $E\left(\xi_{1}\right) < E\left(\xi_{2}\right), D\left(3 \xi_{1}+1\right)>D\left(3 \xi_{2}+1\right)$
$\text{C.}$ $E\left(\xi_{1}\right)>E\left(\xi_{2}\right), \quad D\left(3 \xi_{1}+1\right) < D\left(3 \xi_{2}+1\right)$
$\text{D.}$ $E\left(\xi_{1}\right)>E\left(\xi_{2}\right), \quad D\left(3 \xi_{1}+1\right)>D\left(3 \xi_{2}+1\right)$
随机掷两个质地均匀的正方体骰子,骰子各个面分别标记有 $1 \sim 6$ 共六个数字,记事件 $A=$"骰子向上的点数是 1 和 3 ",事件 $B=$"骰子向上的点数是 3 和 6 ",事件 $C=$"骰子向上的点数含有 3 ",则下列说法正确的是
$\text{A.}$ 事件 A 与事件 $B$ 是相互独立事件
$\text{B.}$ 事件 A 与事件 $C$ 是互斥事件
$\text{C.}$ $P(A)=P(B)=\frac{1}{18}$
$\text{D.}$ $P(C)=\frac{1}{6}$
多选题 (共 4 题 ),每题有多个选项正确
已知随机变量 $X$ 服从正态分布 $N\left(1,3^{2}\right)$ ,则下列结论正确的是( )
$\text{A.}$ $E(X)=1, D(X)=9$
$\text{B.}$ 若 $P(X > 2)=p$ ,则 $P(0 < X \leq 1)=\frac{1}{2}-p$
$\text{C.}$ $P(X > 1)=\frac{1}{2}$
$\text{D.}$ 随机变量 $Y$ 满足 $2 X+Y=4$ ,则 $E(Y)=4$
袋子中共有大小和质地相同的 4 个球,其中 2 个白球和 2 个黑球,从袋中有放回地依次随机摸出 2 个球。甲表示事件"第一次摸到白球",乙表示事件"第二次摸到黑球",丙表示事件"两次都摸到白球",则
$\text{A.}$ 甲与乙互斥
$\text{B.}$ 乙与丙互斥
$\text{C.}$ 甲与乙独立
$\text{D.}$ 甲与乙对立
一个袋中有大小、形状完全相同的 3 个小球,颜色分别为红、黄、蓝,从袋中先后无放回地取出 2 个球,记"第一次取到红球"为事件 $A$ ,"第二次取到黄球"为事件 $B$ ,则
$\text{A.}$ $P(A)=\frac{1}{3}$
$\text{B.}$ $A, B$ 为互斥事件
$\text{C.}$ $P(B \mid A)=\frac{1}{2}$
$\text{D.}$ $A, B$ 相互独立
已知二项式 $\left(x+\frac{1}{x}\right)^{n}=a_{0} x^{n}+a_{1} x^{n-2}+a_{2} x^{n-4}+\mathrm{L}+a_{n} x^{-n}$ 的展开式中各项的系数和为 64 ,则下列说法正确的是
$\text{A.}$ 展开式中的常数项为 1
$\text{B.}$ $n=6$
$\text{C.}$ 展开式中二项式系数最大的项是第四项
$\text{D.}$ 展开式中 $x$ 的指数均为偶数
填空题 (共 4 题 ),请把答案直接填写在答题纸上
某研究机构采访了"一带一路"沿线 20 国的青年,让他们用一个关键词表达对中国的印
象,使用频率前 12 的关键词为:高铁、移动支付、网购、共享单车、一带一路、无人机、大熊猫、广场舞、中华美食、长城、京剧、美丽乡村。其中使用频率排前四的关键词"高铁、移动支付、网购、共享单车"也成为了他们眼中的"新四大发明".从这 12 个关键词中选择 3 个不同的关键词,且至少包含一个"新四大发明"关键词的选法种数为 $\qquad$ (用数字作答)。
已知随机变量 $X: B(2, p)$ ,若 $P(X \geq 1)=\frac{7}{16}$ ,则 $p=$ $\qquad$ .
在二项式 $(1-3 x)^{n}$ 的展开式中,若所有项的系数之和等于 64 ,那么在这个展开式中, $x^{2}$ 项的系数是 $\qquad$ .(用数字作答)
一位飞镖运动员向一个目标投掷三次,记事件 $A_{i}=$"第 i 次命中目标"$(i=1,2,3)$ ,
$P\left(A_{1}\right)=\frac{1}{8}, \quad P\left(A_{i+1} \mid A_{i}\right)=2 P\left(A_{i}\right), \quad P\left(A_{i+1} \mid \overline{A_{i}}\right)=\frac{1}{8}(i=1,2)$ ,则 $P\left(A_{3}\right)=$ $\qquad$ .
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
2025年初,新型冠状病毒疫情牵动着全国人民的心,某市根据上级要求,在本市某人民医院要选出护理外科、心理治疗方面的专家4人与省专家组一起赶赴武汉参加救助工作,该医院现有3名护理专家 $A_1, A_2$ , $A_3, 5$ 名外科专家 $B_1, B_2, B_3, B_4, B_5, 2$ 名心理治疗专家 $C_1, C_2$ .
(1)求 4 人中有 1 位外科专家, 1 位心理治疗师的概率;
(2)求至少含有 2 位外科专家,且外科专家 $B_1$ 和护理专家 $A_1$ 不能同时被选的概率.
在二项式 $\left(\frac{1}{2 x}+\sqrt{x}\right)^n$ 的展开式中, $\qquad$ -给出下列条件:
① 若展开式前三项的二项式系数的和等于 46;
② 所有奇数项的二项式系数的和为 256 ;
③ 若展开式中第 7 项为常数项。
试在上面三个条件中选择一个补充在上面的横线上,并且完成下列问题:
(1)求展开式中二项式系数最大的项;
(2)求展开式的常数项.
(备注:如果多个条件分别解得,按第一个条件计分)
假设有两个密闭的盒子,第一个盒子里装有 3 个白球 2 个红球,第二个盒子里装有 2 个白球 4 个红球,这些小球除颜色外完全相同.
(1)每次从第一个盒子里随机取出一个球,取出的球不再放回,经过两次取球,求取出的两球中有红球的条件下,第二次取出的是红球的概率;
(2)若先从第一个盒子里随机取出一个球放入第二个盒子中,摇匀后,再从第二个盒子里随机取出一个球,求从第二个盒子里取出的球是红球的概率.
袋子中有 8 张水果卡片,其中 4 张苹果卡片, 4 张梨子卡片,消费者从该袋子中不放回地随机抽取 4 张卡片,若抽到的 4 张卡片都是同一种水果,则获得一张 10 元代金券;若抽到的 4 张卡片中恰有 3 张卡片是同一种水果,则获得一张 5 元代金券;若抽到的 4 张卡片是其他情况,则不获得任何奖励。
(1)求某位消费者在一次抽奖活动中抽到的 4 张卡片都是苹果卡片的概率;
(2)记随机变量 $X$ 为某位消费者在一次抽奖活动中获得代金券的金额数,求 $X$ 的分布列和数学期望 $E(X)$ ;
(3)该商家规定,每位消费者若想再次参加该项抽奖活动,则需支付 2 元.若你是消费者,是否愿意再次参加该项抽奖活动?请说明理由.
为了丰富在校学生的课余生活,某校举办了一次趣味运动会活动,学校设置项目 $A^{\prime}$"毛毛虫旱地龙舟"和项目 $B^{\prime \prime}$ 袋鼠接力跳"。甲、乙两班每班分成两组,每组参加一个项目,进行班级对抗赛。每一个比赛项目均采取五局三胜制(即有一方先胜 3 局即获胜,比赛结束),假设在项目 $A$ 中甲班每一局获胜的概率为 $\frac{2}{3}$ ,在项目 $B$ 中甲班每一局获胜的概率为 $\frac{1}{2}$ ,且每一局之间没有影响.
(1)求甲班在项目 $A$ 中获胜的概率;
(2)设甲班获胜的项目个数为 $X$ ,求 $X$ 的分布列及数学期望.
某学校为了迎接党的二十大召开,增进全体教职工对党史知识的了解,组织开展党史知识竞赛活动并以支部为单位参加比赛。现有两组党史题目放在甲、乙两个纸箱中,甲箱有 5 个选择题和 3 个填空题,乙箱中有 4 个选择题和 3 个填空题,比赛中要求每个支部在甲或乙两个纸箱中随机抽取两题作答.每个支部先抽取一题作答,答完后题目不放回纸箱中,再抽取第二题作答,两题答题结束后,再将这两个题目放回原纸箱中.
(1)如果第一支部从乙箱中抽取了 2 个题目,求第 2 题抽到的是填空题的概率;
(2)若第二支部从甲箱中抽取了 2 个题目,答题结束后错将题目放入了乙箱中,接着第三支部答题,第三支部抽取第一题时,从乙箱中抽取了题目.已知第三支部从乙箱中取出的这个题目是选择题,求第二支部从甲箱中取出的是 2 个选择题的概率.