单选题 （共 10 题 ），每题只有一个选项正确
$\frac{1}{6}$ 的相反数是
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $-6$
$\text{C.}$ $6$
$\text{D.}$ $-\frac{1}{6}$
下列运算一定正确的是
$\text{A.}$ $\left(a^2 b^3\right)^2=a^4 b^6$
$\text{B.}$ $3 b^2+b^2=4 b^4$
$\text{C.}$ $\left(a^4\right)^2=a^6$
$\text{D.}$ $a^3 \cdot a^3=a^9$
下列图形中既是轴对称图形又是中心对称图形的是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$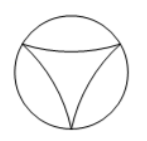 
$\text{D.}$ 
抛物线 $y=2(x+9)^2-3$ 的顶点坐标是
$\text{A.}$ $(9,-3)$
$\text{B.}$ $(-9,-3)$
$\text{C.}$ $(9,3)$
$\text{D.}$ $(-9,3)$
方程 $\frac{2}{x-3}=\frac{3}{x}$ 的解为
$\text{A.}$ $x=3$
$\text{B.}$ $x=-9$
$\text{C.}$ $x=9$
$\text{D.}$ $x=-3$
如图, $A D, B C$ 是 $\odot O$ 的直径, 点 $P$ 在 $B C$ 的延长线上, $P A$ 与 $\odot O$ 相切于点 $A$, 连接 $B D$, 若 $\angle P=40^{\circ}$, 则 $\angle A D B$ 的度数为
$\text{A.}$ $65^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $25^{\circ}$
某种商品原来每件售价为 150 元, 经过连续两次降价后, 该种商品每件售价为 96 元, 设平均每次降价 的百分率为 $x$, 根据随意, 所列方程正确的是
$\text{A.}$ $150\left(1-x^2\right)=96$
$\text{B.}$ $150(1-x)=96$
$\text{C.}$ $150(1-x)^2=96$
$\text{D.}$ $150(1-2 x)=96$
如图, $A B / / C D, A C, B D$ 相交于点 $E, A E=1, E C=2, D E=3$, 则 $B D$ 的长为
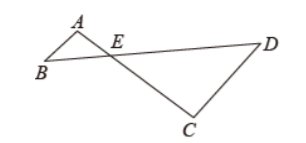
$\text{A.}$ $\frac{3}{2}$
$\text{B.}$ $4$
$\text{C.}$ $\frac{9}{2}$
$\text{D.}$ $6$
一辆汽车油箱中剩余的油量 $y(\mathrm{~L})$ 与已行驶的路程 $x(\mathrm{~km})$ 的对应关系如图所示, 如果这辆汽车每千米 的耗油量相同, 当油箱中剩余的油量为 $35 \mathrm{~L}$ 时, 那么该汽车已行驶的路程为
$\text{A.}$ $150 km$
$\text{B.}$ $165 km$
$\text{C.}$ $125 km$
$\text{D.}$ $350 km$
填空题 （共 10 题 ），请把答案直接填写在答题纸上
风能是一种清洁能源, 我国风能储量很大, 仅陆地上风能储量效有 253000 兆瓦, 用科学记数法表示为 （ ） 兆瓦.
在函数 $y=\frac{x}{5 x+3}$ 中, 自变量 $x$ 的取值范围是
计算 $\sqrt{3}+3 \sqrt{\frac{1}{3}}$ 的结果是
把多项式 $m n^2-9 m$ 分解因式的结果是
不等式组 $\left\{\begin{array}{l}3 x+4 \geq 0, \\ 4-2 x < -1\end{array}\right.$ 的解集是
已知反比例函数 $y=-\frac{6}{x}$ 的图象经过点 $(4, a)$, 则 $a$ 的值为
在 $\triangle A B C$ 中, $A D$ 为边 $B C$ 上的高, $\angle A B C=30^{\circ}, \angle C A D=20^{\circ}$, 则 $\angle B A C$ 是 （ ） 度.
同时抛郑两枚质地均匀的硬币, 一枚硬币正面向上，一枚硬币反面向上的概率是
一个扇形的面积为 $7 \pi \mathrm{cm}^2$, 半径为 $6 \mathrm{~cm}$, 则此扇形的圆心角是 （ ） 度.
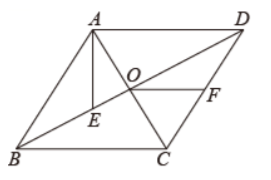
如图, 菱形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $O$, 点 $E$ 在 $O B$ 上, 连接 $A E$, 点 $F$ 为 $C D$ 的中点, 连 接 $O F$, 若 $A E=B E, O E=3, O A=4$, 则线段 $O F$ 的长为
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
先化简, 再求代数式 $\left(\frac{1}{x-1}-\frac{x-3}{x^2-2 x+1}\right) \div \frac{2}{x-1}$ 的值, 其中 $x=2 \cos 45^{\circ}+1$.
如图, 方格纸中每个小正方形的边长均为 $1, \triangle A B C$ 的顶点和线段 $E F$ 的端点均在小正方形的顶点上.
(1) 在方格纸中面出 $\triangle A D C$, 使 $\triangle A D C$ 与 $\triangle A B C$ 关于直线 $A C$ 对称 (点 $D$ 在小正方形的顶点上);
(2) 在方格纸中画出以线段 $E F$ 为一边的平行四边形 $E F G H$ (点 $G$, 点 $H$ 均在小正方形的顶点上), 且 平行四边形 $E F G H$ 的面积为 4 . 连接 $D H$, 请直接写出线段 $D H$ 的长.
民海中学开展以 “我最喜欢的健身活动” 为主题的调查活动, 围绕 “在跑步类、球类、武术类、操舞 类四类健身活动中, 你最喜欢哪一类? (必选且只选一类)” 的问题, 在全校范围内随机抽取部分学生进 行问卷调查, 将调查结果整理后绘制成如图所示的不完整的条形统计图, 其中最喜欢操舞类的学生人数占 所调查人数的 $25 \%$. 请你根据图中提供的信息解答下列问题:
(1) 在这次调查中, 一共抽取了多少名学生?
(2) 请通过计算补全条形统计图;
(3) 若民海中学共有 1600 名学生, 请你估计该中学最喜欢球类的学生共有多少名.
已知矩形 $A B C D$ 对角线 $A C, B D$ 相交于点 $O$, 点 $E$ 是边 $A D$ 上一点, 连接 $B E, C E, O E$, 且
$$
B E=C E .
$$
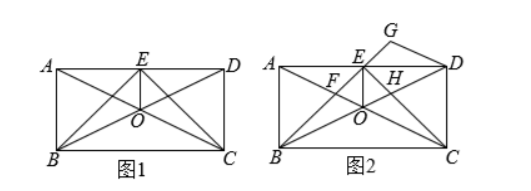
(1) 如图 1, 求证: $\triangle B E O \cong \triangle C E O$;
(2) 如图 2, 设 $B E$ 与 $A C$ 相交于点 $F, C E$ 与 $B D$ 相交于点 $H$, 过点 $D$ 作 $A C$ 的平行线交 $B E$ 的延长线 于点 $G$, 在不添加任何辅助线的情况下, 请直接写出图 2 中的四个三角形 ( $\triangle A E F$ 除外), 使写出的每个 三角形的面积都与 $\triangle A E F$ 的面积相等.
绍云中学计划为绘画小组购买某种品牌的 $A 、 B$ 两种型号的颜料, 若购买 1 盒 $A$ 种型号的颜料和 2 盒 $B$ 种型号的颜料需用 56 元; 若购买 2 盒 $A$ 种型号的颜料和 1 盒 $B$ 种型号的颜料需用 64 元.
(1) 求每盒 $A$ 种型号的颜料和每盒 $B$ 种型号的颜料各多少元;
(2) 绍云中学决定购买以上两种型号的颜料共 200 盒, 总费用不超过 3920 元, 那么该中学最多可以购买
多少盒 $A$ 种型号的颜料?
已知 $C H$ 是 $\odot O$ 的直径, 点 $A$, 点 $B$ 是 $\odot O$ 上的两个点, 连接 $O A, O B$, 点 $D$, 点 $E$ 分别是半径 $O A, O B$ 的中点, 连接 $C D, C E, B H$, 且 $\angle A O C=2 \angle C H B$.
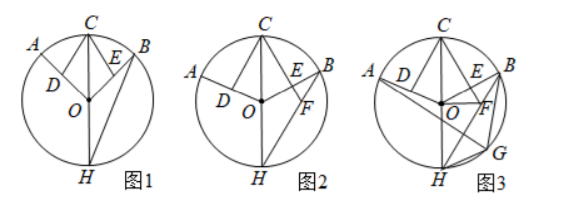
(1) 如图 1, 求证: $\angle O D C=\angle O E C$;
(2) 如图 2, 延长 $C E$ 交 $B H$ 于点 $F$, 若 $C D \perp O A$, 求证: $F C=F H$;
(3) 如图 3, 在 (2) 的条件下, 点 $G$ 是 $B H$ 上一点, 连接 $A G, B G, H G, O F$, 若 $A G: B G=5: 3$, $H G=2$, 求 $O F$ 的长.
在平面直角坐标系中, 点 $O$ 为坐标原点, 抛物线 $y=a x^2+b$ 经过点 $A\left(\frac{5}{2}, \frac{21}{8}\right)$, 点 $B\left(\frac{1}{2},-\frac{3}{8}\right)$, 与 $y$ 轴交于点 $C$.
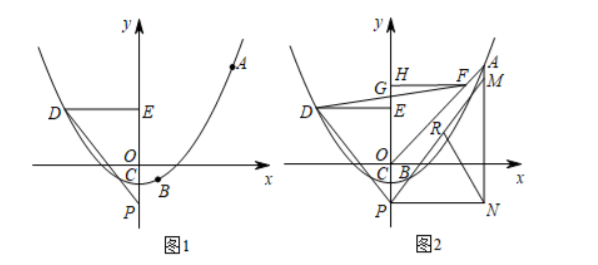
(1) 求 $a, b$ 的值;
(2) 如图 1, 点 $D$ 在该拋物线上, 点 $D$ 横坐标为 $-2$, 过点 $D$ 向 $y$ 轴作垂线, 垂足为点 $E$. 点 $P$ 为 $y$ 轴 负半轴上的一个动点, 连接 $D P$ 、设点 $P$ 的纵坐标为 $t, \triangle D E P$ 的面积为 $S$, 求 $S$ 关于 $t$ 的函数解析式 (不 要求写出自变量 $t$ 的取值范围);
(3) 如图 2, 在 (2) 的条件下, 连接 $O A$, 点 $F$ 在 $O A$ 上, 过点 $F$ 向 $y$ 轴作垂线, 垂足为点 $H$, 连接 $D F$ 交 $y$ 轴于点 $G$, 点 $G$ 为 $D F$ 的中点, 过点 $A$ 作 $y$ 轴的平行线与过点 $P$ 所作的 $x$ 轴的平行线相交于点 $N$, 连 接 $C N, P B$, 延长 $P B$ 交 $A N$ 于点 $M$, 点 $R$ 在 $P M$ 上, 连接 $R N$, 若 $3 C P=5 G E$, $\angle P M N+\angle P D E=2 \angle C N R$, 求直线 $R N$ 的解析式.