已知矩形 $A B C D$ 对角线 $A C, B D$ 相交于点 $O$, 点 $E$ 是边 $A D$ 上一点, 连接 $B E, C E, O E$, 且
$$
B E=C E .
$$
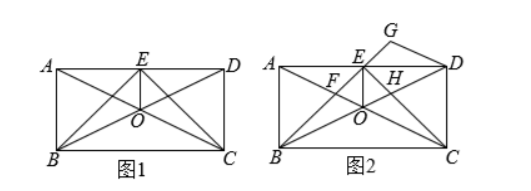
(1) 如图 1, 求证: $\triangle B E O \cong \triangle C E O$;
(2) 如图 2, 设 $B E$ 与 $A C$ 相交于点 $F, C E$ 与 $B D$ 相交于点 $H$, 过点 $D$ 作 $A C$ 的平行线交 $B E$ 的延长线 于点 $G$, 在不添加任何辅助线的情况下, 请直接写出图 2 中的四个三角形 ( $\triangle A E F$ 除外), 使写出的每个 三角形的面积都与 $\triangle A E F$ 的面积相等.
$$
B E=C E .
$$

(1) 如图 1, 求证: $\triangle B E O \cong \triangle C E O$;
(2) 如图 2, 设 $B E$ 与 $A C$ 相交于点 $F, C E$ 与 $B D$ 相交于点 $H$, 过点 $D$ 作 $A C$ 的平行线交 $B E$ 的延长线 于点 $G$, 在不添加任何辅助线的情况下, 请直接写出图 2 中的四个三角形 ( $\triangle A E F$ 除外), 使写出的每个 三角形的面积都与 $\triangle A E F$ 的面积相等.