在平面直角坐标系中, 点 $O$ 为坐标原点, 抛物线 $y=a x^2+b$ 经过点 $A\left(\frac{5}{2}, \frac{21}{8}\right)$, 点 $B\left(\frac{1}{2},-\frac{3}{8}\right)$, 与 $y$ 轴交于点 $C$.


(1) 求 $a, b$ 的值;
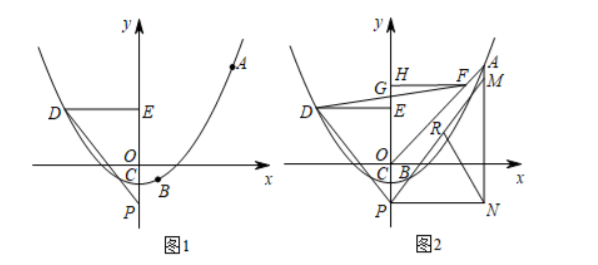
(2) 如图 1, 点 $D$ 在该拋物线上, 点 $D$ 横坐标为 $-2$, 过点 $D$ 向 $y$ 轴作垂线, 垂足为点 $E$. 点 $P$ 为 $y$ 轴 负半轴上的一个动点, 连接 $D P$ 、设点 $P$ 的纵坐标为 $t, \triangle D E P$ 的面积为 $S$, 求 $S$ 关于 $t$ 的函数解析式 (不 要求写出自变量 $t$ 的取值范围);
(3) 如图 2, 在 (2) 的条件下, 连接 $O A$, 点 $F$ 在 $O A$ 上, 过点 $F$ 向 $y$ 轴作垂线, 垂足为点 $H$, 连接 $D F$ 交 $y$ 轴于点 $G$, 点 $G$ 为 $D F$ 的中点, 过点 $A$ 作 $y$ 轴的平行线与过点 $P$ 所作的 $x$ 轴的平行线相交于点 $N$, 连 接 $C N, P B$, 延长 $P B$ 交 $A N$ 于点 $M$, 点 $R$ 在 $P M$ 上, 连接 $R N$, 若 $3 C P=5 G E$, $\angle P M N+\angle P D E=2 \angle C N R$, 求直线 $R N$ 的解析式.