已知 $C H$ 是 $\odot O$ 的直径, 点 $A$, 点 $B$ 是 $\odot O$ 上的两个点, 连接 $O A, O B$, 点 $D$, 点 $E$ 分别是半径 $O A, O B$ 的中点, 连接 $C D, C E, B H$, 且 $\angle A O C=2 \angle C H B$.


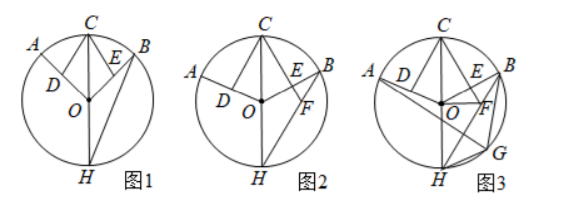
(1) 如图 1, 求证: $\angle O D C=\angle O E C$;
(2) 如图 2, 延长 $C E$ 交 $B H$ 于点 $F$, 若 $C D \perp O A$, 求证: $F C=F H$;
(3) 如图 3, 在 (2) 的条件下, 点 $G$ 是 $B H$ 上一点, 连接 $A G, B G, H G, O F$, 若 $A G: B G=5: 3$, $H G=2$, 求 $O F$ 的长.