单选题 (共 10 题 ),每题只有一个选项正确
$-2022$ 的相反数是
$\text{A.}$ 2022
$\text{B.}$ $-2022$
$\text{C.}$ $-\frac{1}{2022}$
$\text{D.}$ $\frac{1}{2022}$
下列计算正确的是 ( )
$\text{A.}$ $a^3+a=a^4$
$\text{B.}$ $a^6 \div a^2=a^3$
$\text{C.}$ $\left(a^2\right)^3=a^5$
$\text{D.}$ $a^3 \cdot a=a^4$
据国家医保局最新消息, 全国统一的医保信息平台已全面建成, 在全国 31 个省份和新 疆生产建设兵团全域上线, 为 1360000000 参保人提供医保服务, 医保信息化标准化取得里 程碑式突破. 数 1360000000 用科学记数法表示为()
$\text{A.}$ $1.36 \times 10^7$
$\text{B.}$ $13.6 \times 10^8$
$\text{C.}$ $1.36 \times 10^9$
$\text{D.}$ $0.136 \times 10^{10}$
开学前,根据学校防疫要求,小宁同学连续14天进行了体温测量,结果统计如下表

这 14 天中, 小宁体温的众数和中位数分别为()
$\text{A.}$ $36.6^{\circ} \mathrm{C}, 36.4^{\circ} \mathrm{C}$
$\text{B.}$ $36.5^{\circ} \mathrm{C}, 36.5^{\circ} \mathrm{C}$
$\text{C.}$ $36.8^{\circ} \mathrm{C}, 36.4^{\circ} \mathrm{C}$
$\text{D.}$ $36.8^{\circ} \mathrm{C}, \quad 36.5^{\circ} \mathrm{C}$
已知圆锥的底面半径为 $4 \mathrm{~cm}$, 母线长为 $6 \mathrm{~cm}$, 则圆雉的侧面积为
$\text{A.}$ $36 \pi \mathrm{cm}^2$
$\text{B.}$ $24 \pi \mathrm{cm}^2$
$\text{C.}$ $16 \pi \mathrm{cm}^2$
$\text{D.}$ $12 \pi \mathrm{cm}^2$
如图, 在 $R f \mathrm{~V} A B C$ 中, $D$ 为斜边 $A C$ 的中点, $E$ 为 $B D$ 上一点, $F$ 为 $C E$ 中点. 若 $A E=A D, D F=2$, 则 $B D$ 的长为
$\text{A.}$ $2 \sqrt{2}$
$\text{B.}$ 3
$\text{C.}$ $2 \sqrt{3}$
$\text{D.}$ 4
我国古代数学名著《九章算术》中记载: “粟米之法: 粟率五十; 粝米三十. 今有米在 十斗桶中, 不知其数. 满中添粟而春之, 得米七斗. 问故米几何?” 意思为: 50 斗谷子能 出 30 斗米, 即出米率为 $\frac{3}{5}$. 今有米在容量为 10 斗的桶中, 但不知道数量是多少. 再向桶 中加满谷子, 再春成米, 共得米 7 斗. 问原来有米多少斗? 如果设原来有米 $x$ 斗, 向桶中 加谷子 $y$ 斗, 那么可列方程组为
$\text{A.}$ $\left\{\begin{array}{l}x+y=10 \\ x+\frac{3}{5} y=7\end{array}\right.$
$\text{B.}$ $\left\{\begin{array}{l}x+y=10 \\ \frac{3}{5} x+y=7\end{array}\right.$
$\text{C.}$ $\left\{\begin{array}{l}x+y=7 \\ x+\frac{5}{3} y=10\end{array}\right.$
$\text{D.}$ $\left\{\begin{array}{l}
x+y=7 \\
\frac{5}{3} x+y=10
\end{array}\right.$
点 $A\left(m-1, y_1\right), B\left(m, y_2\right)$ 都在二次函数 $y=(x-1)^2+n$ 的图象上. 若 $y_1 < y_2$, 则 $m$ 的 取值范围为
$\text{A.}$ $m>2$
$\text{B.}$ $m>\frac{3}{2}$
$\text{C.}$ $m < 1$
$\text{D.}$ $\frac{3}{2} < m < 2$
将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形$ABCD$内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出
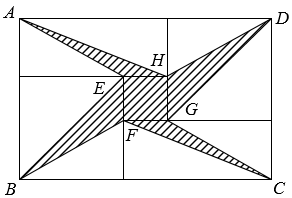
$\text{A.}$ 正方形纸片的面积
$\text{B.}$ 四边形EFGH的面积
$\text{C.}$ VBEF的面积
$\text{D.}$ $\triangle AEH$的面积
填空题 (共 6 题 ),请把答案直接填写在答题纸上
一个不透明的袋子里装有 5 个红球和 6 个白球, 它们除颜色外其余都相同. 从袋中任 意摸出一个球是红球的概率为
定义一种新运算: 对于任意的非零实数 $a, b, a \otimes b=\frac{1}{a}+\frac{1}{b}$. 若 $(x+1) \otimes x=\frac{2 x+1}{x}$, 则 $x$ 的值为
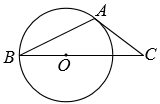
如图, 在 $\triangle A B C$ 中, $A C=2, B C=4$, 点 $O$ 在 $B C$ 上, 以 $O B$ 为半径的圆与 $A C$ 相切于点 $A, D$ 是 $B C$ 边上的动点, 当 $\triangle A C D$ 为直角三角形时, $A D$ 的长为
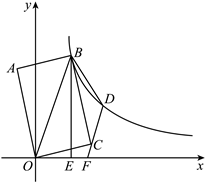
如图, 四边形 $O A B C$ 为矩形, 点 $A$ 在第二象限, 点 $A$ 关于 $O B$ 的对称点为点 $D$, 点 $B$, $D$ 都在函数 $y=\frac{6 \sqrt{2}}{x}(x>0)$ 的图象上, $B E \perp x$ 轴于点 $E$. 若 $D C$ 的延长线交 $x$ 轴于点 $F$, 当矩形 $O A B C$ 的面积为 $9 \sqrt{2}$ 时, $\frac{E F}{O E}$ 的值为 , 点 $F$ 的坐标为
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1) 计算: $(x+1)(x-1)+x(2-x)$.
(2) 解不等式组: $\left\{\begin{array}{c}4 x-3>9 \\ 2+x \geq 0\end{array}\right.$
图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段 的端点均在格点上,分别按要求画出图形.
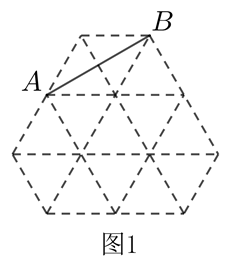

(1) 在图 1 中画出等腰三角形 $A B C$, 且点 $C$ 在格点上. (画出一个即可)
(2) 在图 2 中画出以 $A B$ 为边的菱形 $A B D E$, 且点 $D, E$ 均在格点上.
如图, 正比例函数 $y=-\frac{2}{3} x$ 的图像与反比例函数 $y=\frac{k}{x}(k \neq 0)$ 的图像都经过点 $A(a, 2)$
(1)求点 $A$ 的坐标和反比例函数表达式.
(2) 若点 $P(m, n)$ 在该反比例函数图像上, 且它到 $y$ 轴距离小于 3 , 请根据图像直接写出 $n$ 的取值范围.

小聪、小明参加了100米跑的5期集训,每期集训结束时进行测试.根据他们集训时间、测试成绩绘制成如下两个统计图.
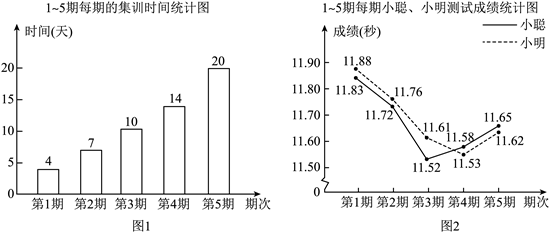
根据图中信息,解答下列问题:
(1)这5期的集训共有多少天?
(2)哪一期小聪的成绩比他上一期的成绩进步最多?进步了多少秒?
(3)根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,简要说说你的想法.
每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
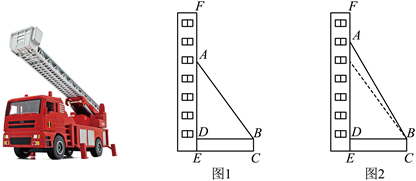
(1) 若 $\angle A B D=53^{\circ}$, 求此时云梯 $A B$ 的长.
(2) 如图 2, 若在建筑物底部 $E$ 的正上方 $19 \mathrm{~m}$ 处突发险情, 请问在该消防车不移动位置的 前提下, 云梯能否伸到险情处? 请说明理由.
(参考数据: $\sin 53^{\circ} \approx 0.8, \cos 53^{\circ} \approx 0.6, \tan 53^{\circ} \approx 1.3$ )
为了落实劳动教育, 某学校邀请农科院专家指导学生进行小番茄的种植, 经过试验, 其平 均单株产量 $y$ 千克与每平方米种植的株数 $x(2 \leq x \leq 8$, 且 $x$ 为整数) 构成一种函数关 系. 每平方米种植 2 株时, 平均单株产量为 4 千克; 以同样的栽培条件, 每平方米种植的 株数每增加 1 株, 单株产量减少 $0.5$ 千克.
(1) 求 $y$ 关于 $x$ 的函数表达式.
(2) 每平方米种植多少株时, 能获得最大的产量? 最大产量为多少千克?
(1) 如图 1, 在 $\mathrm{V} A B C$ 中, $D, E, F$ 分别为 $A B, A C, B C$ 上的点,
$D E / / B C, B F=C F, A F$ 交 $D E$ 于点 $G$, 求证: $D G=E G$.
(2) 如图 2, 在 (1) 的条件下, 连接 $C D, C G$. 若 $C G \perp D E, C D=6, A E=3$, 求 $\frac{D E}{B C}$ 的值.
(3) 如图 3, 在Y $\mathrm{Y} B C D$ 中, $\angle A D C=45^{\circ}, A C$ 与 $B D$ 交于点 $O, E$ 为 $A O$ 上一点, $E G / / B D$ 交 $A D$ 于点 $G, E F \perp E G$ 交 $B C$ 于点 $F$. 若 $\angle E G F=40^{\circ}, F G$ 平分 $\angle E F C, F G=10$, 求 $B F$ 的长.

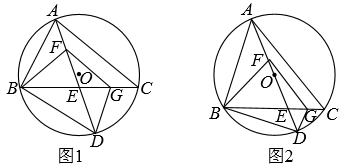
如图 1, 圆 $O$ 为锐角三角形 $A B C$ 的外接圆, 点 $D$ 在 $B C$ 上, $A D$ 交 $B C$ 于点 $E$, 点 $F$ 在 $A E$ 上, 满足 $\angle A F B-\angle B F D=\angle A C B, F G / / A C$ 交 $B C$ 于点 $G, B E=F G$, 连结 $B D, D G$. 设 $\angle A C B=\alpha$.
(1) 用含 $\alpha$ 的代数式表示 $\angle B F D$.
(2) 求证: $\triangle B D E \cong \triangle F D G$.
(3) 如图 2, $A D$ 为 e $O$ 的直径.
① 当 $A B$ 的长为 2 时, 求 $A C$ 的长.
②当 $O F: O E=4: 11$ 时, 求 $\cos \alpha$ 的值.