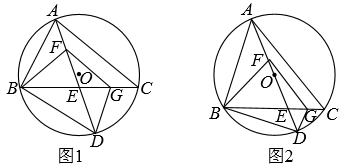
如图 1, 圆 $O$ 为锐角三角形 $A B C$ 的外接圆, 点 $D$ 在 $B C$ 上, $A D$ 交 $B C$ 于点 $E$, 点 $F$ 在 $A E$ 上, 满足 $\angle A F B-\angle B F D=\angle A C B, F G / / A C$ 交 $B C$ 于点 $G, B E=F G$, 连结 $B D, D G$. 设 $\angle A C B=\alpha$.
(1) 用含 $\alpha$ 的代数式表示 $\angle B F D$.
(2) 求证: $\triangle B D E \cong \triangle F D G$.
(3) 如图 2, $A D$ 为 e $O$ 的直径.
① 当 $A B$ 的长为 2 时, 求 $A C$ 的长.
②当 $O F: O E=4: 11$ 时, 求 $\cos \alpha$ 的值.