单选题 (共 5 题 ),每题只有一个选项正确
如图, 已知点 $P_0$ 的坐标为 $(1,0)$, 将点 $P_0$ 绕着原点 $O$ 按逆时针方向旋转 $30^{\circ}$ 得到点 $P_1$,延长 $O P_1$ 到 $P_2$, 使得 $O P_2=2 O P_1$; 再将点 $P_2$ 绕着原点 $O$ 按逆时针方向旋转 30 得到 $O P_3$, 延长 $O P_3$ 到 $P_4$, 使得 $O P_4=2 OP _3 \ldots \ldots$ 如此继续下去, 点 $P_{2023}$ 坐标为
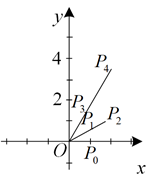
$\text{A.}$ $\left(-2^{1010}, \sqrt{3} \cdot 2^{1010}\right)$
$\text{B.}$ $\left(0,2^{1011}\right)$
$\text{C.}$ $\left(2^{1010}, \sqrt{3} \cdot 2^{1010}\right)$
$\text{D.}$ $\left(\sqrt{3} \cdot 2^{1010}, 2^{1010}\right)$
如图, 已知菱形 $O A B C$ 的顶点 $O(0,0), B(2,2)$, 若菱形绕点 $O$ 逆时针旋转, 每秒旋转 $45^{\circ}$ ,则第 60 秒时,菱形的对角线交点 D 的坐标为

$\text{A.}$ $(1,-1)$
$\text{B.}$ $(-1,-1)$
$\text{C.}$ $(\sqrt{2}, 0)$
$\text{D.}$ $(0,-\sqrt{2})$
在平面直角坐标系中, 若干个半径为 1 个单位长度, 圆心角为 $60^{\circ}$ 的扇形组成一条连续的曲线, 点 $P$ 从原点 $O$ 出发, 沿这条曲线向右上下起伏运动, $P$ 点在直线上的速度为 1 个单位长度/秒, 在弧线上的速度为 $\frac{\pi}{3}$ 个单位长度/秒, 则 2022 秒时, 点 $P$ 的坐标是
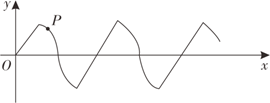
$\text{A.}$ $(1011,0)$
$\text{B.}$ $\left(1010, \frac{\sqrt{3}}{2}\right)$
$\text{C.}$ $\left(1011,-\frac{\sqrt{3}}{2}\right)$
$\text{D.}$ $\left(1010,-\frac{\sqrt{3}}{2}\right)$
如图所示, 在平面直角坐标系中, 将点 $A(-1,0)$ 做如下的连续平移, $A(-1,0) \rightarrow A_l(-1$, 1) $\rightarrow A_2(2,1) \rightarrow A_3(2,-4) \rightarrow A_4(-5,-4) \rightarrow A_5(-5,5) \ldots$, 按此规律平移下去, 则 $A_{102}$的点坐标是
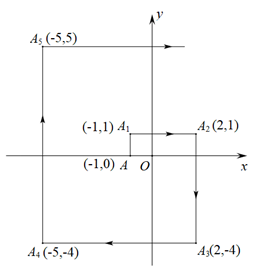
$\text{A.}$ $(100,101)$
$\text{B.}$ $(101,100)$
$\text{C.}$ $(102,101)$
$\text{D.}$ $(103,102)$
如图, 在一单位为 1 的方格纸上, $\triangle A_1 A_2 A_3, \triangle A_3 A_4 A_5, \triangle A_5 A_6 A_7 \ldots$, 都是斜边在 $x$ 轴上, 斜边长分别为 $2,4,6, \ldots$ 的等腰直角三角形, 若 $A_l A_2 A_3$ 的顶点坐标分别为 $A_l(2,0), A_2(1$, -1), $A_3(0,0)$, 则依图中所示规律, $A_{2022}$ 的坐标为
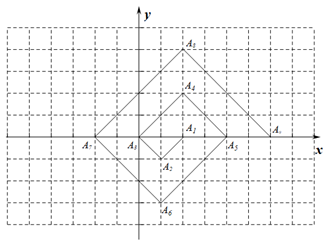
$\text{A.}$ $(2,1010)$
$\text{B.}$ $(2,1011)$
$\text{C.}$ $(1,-1010)$
$\text{D.}$ $(1,-1011)$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
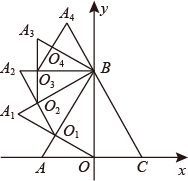
如图, 边长为 4 的等边 $V A B C, A C$ 边在 $x$ 轴上, 点 $B$ 在 $y$ 轴的正半轴上, 以 $O B$ 为边作等边 $\triangle O B A_1$, 边 $O A_1$ 与 $A B$ 交于点 $O_1$, 以 $O_1 B$ 为边作等边 $\triangle O_1 B A_2$, 边 $O_1 A_2$ 与 $A_1 B$ 交于点 $O_2$, 以 $O_2 B$ 为边作等边 $\triangle O_2 B A_3$, 边 $O_2 A_3$ 与 $A_2 B$ 交于点 $O_3$, , , 依此规律继续作等边 $\triangle O_{n-1} B A_n$,则 $A_{2021}$ 的横坐标 .
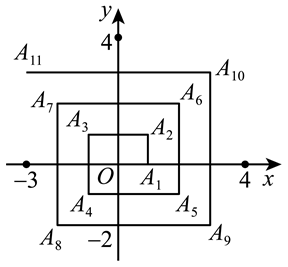
如图, 已知 $A_1(1,0), A_2(1,1), A_3(-1,1), A_4(-1,-1), A_5(2,-1) \ldots$, 则 $A_{2021}$ 的坐标是
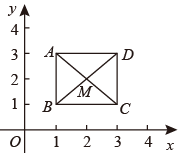
如图, 已知正方形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $M$, 顶点 $A , B, C$ 的坐标分别为 $(1,3)$, $(1,1),(3,1)$, 规定"把正方形 $A B C D$ 先沿 $x$ 轴翻折, 再向右平移 1 个单位"为一次变换, 如此这样, 连续经过 2020 次变换后, 点 $M$ 的坐标变为
如图, 在平面直角坐标系 $x O y$ 中, 正方形 $O A B C$ 的顶点 $A 、 C$ 分别在 $x, y$ 轴上, 且 $A O=1$. 将正方形 $O A B C$ 绕原点 $O$ 顺时针旋转 $90^{\circ}$, 且 $A_1 O=2 A O$, 得到正方形 $O A_1 B_1 C_1$, 再将正方 $O A_1 B_1 C_1$绕原点 $O$ 顺时针旋转 $90^{\circ}$, 且 $A_2 O=2 A_1 O$, 得到正方形 $O A_2 B_2 C_2$, 以此规律, 得到正方形 $O A_{2019} B_{2019} C_{2019}$, 则点 $B_{2019}$ 的坐标为 .
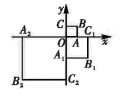
如图所示, 一个机器人从 $O$ 点出发, 向正东方向走 3 m 到达 $A_1$ 点, 再向正北方向走 6 m 到达 $A_2$点, 再向正西方向走 9 m 到达 $A_3$ 点, 再向正南方向走 12 m 到达 $A_4$ 点, 再向正东方向走 15 m 到达 $A_5$ 点, 按照此规律走下去, 相对于点 $O$, 机器人走到 $A_6$ 时, 点 $A_6$ 的坐标是 $\qquad$ , 点 $A_{2022}$的坐标是 .
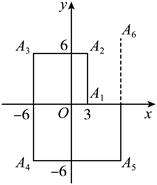
如图, 在平面直角坐标系中, 将边长为 1 的正方形 $O A B C$ 绕点顺时针旋转 $45^{\circ}$ 后得到正方形 $O A_l B_l C_l$, 依此方式, 绕点 $O$ 连续旋转 2022 次得到正方形 $O A_{2022} B_{2022} C_{2022}$, 那么点 $B_{2022}$的坐标是
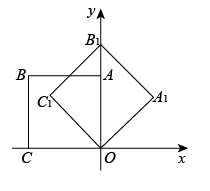
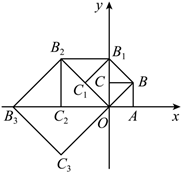
如图, 在平面直角坐标系中放置一菱形 $O A B C$, 已知 $\angle A B C=60^{\circ}$, 点 $B$ 在 $y$ 轴上, $O A=1$,先将菱形 $O A B C$ 沿 $x$ 轴的正方向无滑动翻转, 每次翻转 $60^{\circ}$, 连续翻转 2022 次, 点 $B$ 的落点依次为 $B_1, B_2, B_3, \cdots$, 则 $B_{2022}$ 的横坐标为 .
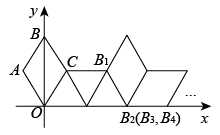
如图, 在平面直角坐标系中有一边长为 1 的正方形 $O A B C$, 边 $O A 、 O C$ 分别在 $x$ 轴、 $y$ 轴上,如果以对角线 $O B$ 为边作第二个正方形 $O B B_1 C_1$, 再以对角线 $O B_1$ 为边作第三个正方形 $O B_1 B_2 C_2 \ldots \ldots$. 照此规律作下去, 则 $O B_{2022}$ 的长为