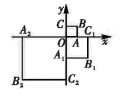
如图, 在平面直角坐标系 $x O y$ 中, 正方形 $O A B C$ 的顶点 $A 、 C$ 分别在 $x, y$ 轴上, 且 $A O=1$. 将正方形 $O A B C$ 绕原点 $O$ 顺时针旋转 $90^{\circ}$, 且 $A_1 O=2 A O$, 得到正方形 $O A_1 B_1 C_1$, 再将正方 $O A_1 B_1 C_1$绕原点 $O$ 顺时针旋转 $90^{\circ}$, 且 $A_2 O=2 A_1 O$, 得到正方形 $O A_2 B_2 C_2$, 以此规律, 得到正方形 $O A_{2019} B_{2019} C_{2019}$, 则点 $B_{2019}$ 的坐标为 .