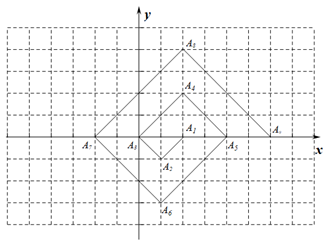
如图, 在一单位为 1 的方格纸上, $\triangle A_1 A_2 A_3, \triangle A_3 A_4 A_5, \triangle A_5 A_6 A_7 \ldots$, 都是斜边在 $x$ 轴上, 斜边长分别为 $2,4,6, \ldots$ 的等腰直角三角形, 若 $A_l A_2 A_3$ 的顶点坐标分别为 $A_l(2,0), A_2(1$, -1), $A_3(0,0)$, 则依图中所示规律, $A_{2022}$ 的坐标为
A
$(2,1010)$
B
$(2,1011)$
C
$(1,-1010)$
D
$(1,-1011)$
E
F