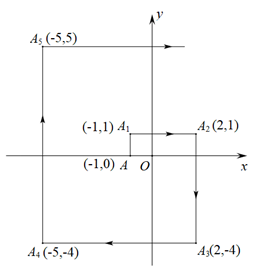
如图所示, 在平面直角坐标系中, 将点 $A(-1,0)$ 做如下的连续平移, $A(-1,0) \rightarrow A_l(-1$, 1) $\rightarrow A_2(2,1) \rightarrow A_3(2,-4) \rightarrow A_4(-5,-4) \rightarrow A_5(-5,5) \ldots$, 按此规律平移下去, 则 $A_{102}$的点坐标是
A
$(100,101)$
B
$(101,100)$
C
$(102,101)$
D
$(103,102)$
E
F