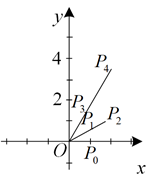
如图, 已知点 $P_0$ 的坐标为 $(1,0)$, 将点 $P_0$ 绕着原点 $O$ 按逆时针方向旋转 $30^{\circ}$ 得到点 $P_1$,延长 $O P_1$ 到 $P_2$, 使得 $O P_2=2 O P_1$; 再将点 $P_2$ 绕着原点 $O$ 按逆时针方向旋转 30 得到 $O P_3$, 延长 $O P_3$ 到 $P_4$, 使得 $O P_4=2 OP _3 \ldots \ldots$ 如此继续下去, 点 $P_{2023}$ 坐标为
A
$\left(-2^{1010}, \sqrt{3} \cdot 2^{1010}\right)$
B
$\left(0,2^{1011}\right)$
C
$\left(2^{1010}, \sqrt{3} \cdot 2^{1010}\right)$
D
$\left(\sqrt{3} \cdot 2^{1010}, 2^{1010}\right)$
E
F