单选题 (共 8 题 ),每题只有一个选项正确
用数轴上的点表示下列各数, 其中与原点距离最近的是
$\text{A.}$ -3
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
下列图案中, 是轴对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
苏州市统计局公布, 2023 年苏州市全年实现地区生产总值约为 2.47 万亿元, 被誉为“最强地级市”. 数据“ 2470000000 000 "用科学记数法可表示为
$\text{A.}$ $2.47 \times 10^{10}$
$\text{B.}$ $247 \times 10^{10}$
$\text{C.}$ $2.47 \times 10^{12}$
$\text{D.}$ $247 \times 10^{12}$
若 $a>b-1$, 则下列结论一定正确的是
$\text{A.}$ $a+1 < b$
$\text{B.}$ $a-1 < b$
$\text{C.}$ $a>b$
$\text{D.}$ $a+1>b$
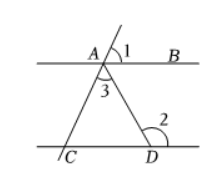
如图, $A B \| C D$, 若 $\angle 1=65^{\circ}, \angle 2=120^{\circ}$, 则 $\angle 3$ 的度数为
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $55^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $65^{\circ}$
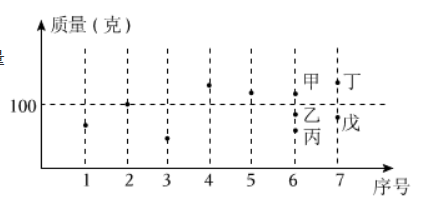
某公司拟推出由7个盲盒组成的套装产品, 现有 10 个盲盒可供选择,统计这 10 个盲盒的质量如图所示. 序号为 1 到 5 号的盲盒已选定, 这 5 个盲盒质量的中位数恰好为 100,6 号盲盒从甲、乙、丙中选择 1 个, 7 号盲盒从丁、戊中选择 1 个, 使选定 7 个盲盒质量的中位数仍为 100 , 可以选择
$\text{A.}$ 甲、丁
$\text{B.}$ 乙、戊
$\text{C.}$ 丙、丁
$\text{D.}$ 丙、戊
如图, 点 $A$ 为反比例函数 $y=-\frac{1}{x}(x < 0)$ 图象上的一点, 连接 $A O$, 过点 $O$ 作 $O A$ 的垂线与反比例函数 $y=\frac{4}{x}(x>0)$ 的图象交于点 $B$, 则 $\frac{A O}{B O}$ 的值为
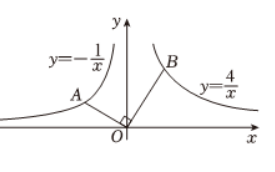
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\frac{1}{3}$
如图, 矩形 $A B C D$ 中, $A B=\sqrt{3}, B C=1$, 动点 $E, F$ 分别从点 $A, C$ 同时出发, 以每秒 1 个单位长度的速度沿 $A B, C D$ 向终点 $B, D$ 运动, 过点 $E, F$ 作直线 $l$, 过点 $A$ 作直线 $l$ 的垂线, 垂足为 $G$, 则 $A G$ 的最大值为

$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $\frac{\sqrt{3}}{2}$
$\text{C.}$ 2
$\text{D.}$ 1
填空题 (共 8 题 ),请把答案直接填写在答题纸上
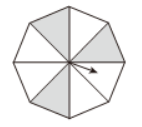
如图, 正八边形转盘被分成八个面积相等的三角形, 任意转动这个转盘一次, 当转盘停止转动时, 指针落在阴影部分的概率是
如图, $\triangle A B C$ 是 $\odot O$ 的内接三角形, 若 $\angle O B C=28^{\circ}$, 则 $\angle A=$

直线 $l_1: y=x-1$ 与 $x$ 轴交于点 $A$, 将直线 $l_1$ 绕点 $A$ 逆时针旋转 $15^{\circ}$, 得到直线 $l_2$, 则直线 $l_2$ 对应的函数表达式是
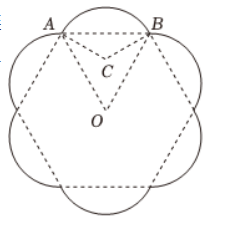
铁艺花窗是园林设计中常见的装饰元素. 如图是一个花瓣造型的花窗示意图, 由六条等弧连接而成, 六条弧所对应的弦构成一个正六边形, 中心为点 $O, \widehat{A B}$ 所在圆的圆心 $C$ 恰好是 $\triangle A B O$ 的内心, 若 $A$ $B=2 \sqrt{3}$, 则花窗的周长 (图中实线部分的长度) $=$ $\qquad$ . (结果保留 $\pi$ )
二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图象过点 $A(0, m), B(1,-m), C(2, n), D(3,-m)$, 其中 $m, n$ 为常数,则 $\frac{m}{n}$ 的值为
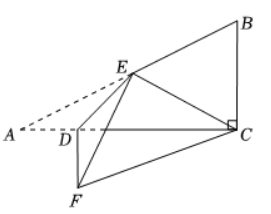
如图, $\triangle A B C$ 中, $\angle A C B=90^{\circ}, C B=5, C A=10$, 点 $D, E$ 分别在 $A C, A B$ 边上, $A E=$ $\sqrt{5} A D$, 连接 $D E$, 将 $\triangle A D E$ 沿 $D E$ 翻折, 得到 $\triangle F D E$, 连接 $C E, C F$. 若 $\triangle C E F$ 的面积是 $\triangle B E C$ 面积的 2 倍, 则 $A D=$
解答题 (共 11 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $|-4|+(-2)^0-\sqrt{9}$.
解方程组: $\left\{\begin{array}{l}2 x+y=7 \\ 2 x-3 y=3\end{array}\right.$.
先化简, 再求值: $\left(\frac{x+1}{x-2}+1\right) \div \frac{2 x^2-x}{x^2-4}$, 其中 $x=-3$.
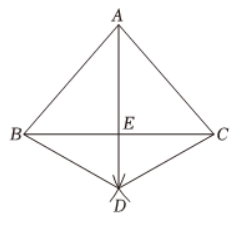
如图, $\triangle A B C$ 中, $A B=A C$, 分别以 $B, C$ 为圆心, 大于 $\frac{1}{2} B C$ 长为半径画弧, 两弧交于点 $D$,连接 $B D, C D, A D, A D$ 与 $B C$ 交于点 $E$.
(1)求证: $\triangle A B D \cong \triangle A C D$ ;
(2) 若 $B D=2, \angle B D C=120^{\circ}$, 求 $B C$ 的长.
一个不透明的盒子里装有4张书签, 分别描绘“春”, “筫”, “秋”, “冬”四个季节, 书签除图案外都相同, 并将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签, 恰好抽到“筫”的概率为 $\qquad$ ;
(2)若从盒子中任意抽取2张书签(先抽取1张书签, 且这张书签不放回, 再抽取1张书签),求抽取的书签恰好1张为“春”,1张为 “秋”的概率.(请用画树状图或列表等方法说明理由)

某校计划在七年级开展阳光体育锻炼活动, 开设以下五个球类项目: $A$ (羽毛球), $B$ (乒乓球), $C$ (篮球), $D$ (排球), $E$ (足球), 要求每位学生必须参加, 且只能选择其中一个项目. 为了了解学生对这五个项目的选择情况, 学校从七年身全体学生中随机抽取部分学生进行问卷调查, 对调查所得到的数据进行整理、描述和分析, 部分信息如下:
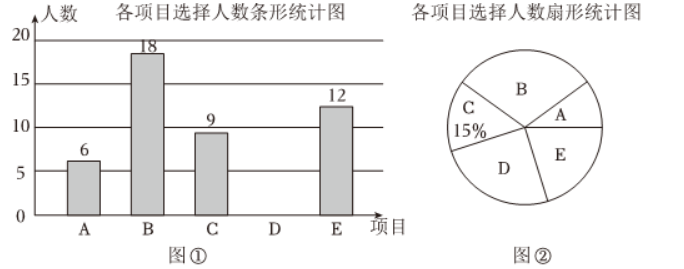
根据上信息, 解决下列问题:
(1) 将图(1)中的条形统计图补充完整(画图并标注相应数据);
(2) 图(2)中项目 $E$ 对应的圆心角的度数为 $\qquad$
(3) 根据抽样调查结果, 请估计本校七年级 800 名学生中选择项目 $B$ (兵乓球) 的人数.
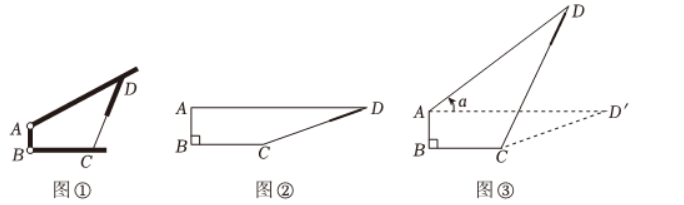
图 ① 是某种可调节支撑架, $B C$ 为水平固定杆, 竖直固定杆 $A B \perp B C$, 活动杆 $A D$ 可绕点 $A$ 旋转, $C D$ 为液压可伸缩支撑杆, 已知 $A B=10 \mathrm{~cm}, B C=20 \mathrm{~cm}, A D=50 \mathrm{~cm}$.
(1)如图 ② , 当活动杆 $A D$ 处于水平状态时, 求可伸缩支撑杆 $C D$ 的长度 (结果保留根号 );
(2) 如图 ③ , 当活动杆 $A D$ 绕点 $A$ 由水平状态按逆时针方向旋转角度 $\alpha$, 且 $\tan \alpha=\frac{3}{4}$ ( $\alpha$ 为锐角 ), 求此时可伸缩支撑杆 $C D$ 的长度 ( 结果保留根号 ).
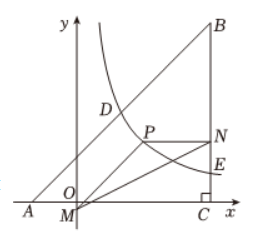
如图, $\triangle A B C$ 中, $A C=B C, \angle A C B=90^{\circ}, A(-2,0), C(6,0)$, 反比例函数 $y=\frac{k}{x}$ $(k \neq 0, x>0)$ 的图象与 $A B$ 交于点 $D(m, 4)$, 与 $B C$ 交于点 $E$.
(1) 求 $m, k$ 的值;
(2) 点 $P$ 为反比例函数 $y=\frac{k}{x}(k \neq 0, x>0)$ 图象上一动点 (点 $P$ 在 $D, E$ 之间运动, 不与 $D, E$ 重合), 过点 $P$ 作 $P M \| A B$, 交 $y$ 轴于点 $M$, 过点 $P$ 作 $P N \| x$ 轴, 交 $B C$ 于点 $N$, 连接 $M N$, 求 $\triangle P M N$ 面积的最大值, 并求出此时点 $P$ 的坐标.
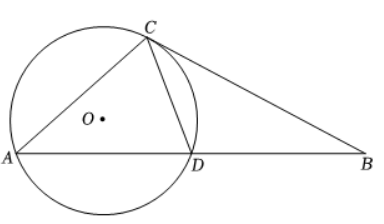
如图, $\triangle A B C$ 中, $A B=4 \sqrt{2}, D$ 为 $A B$ 中点, $\angle B A C=\angle B C D, \cos \angle A$ $D C=\frac{\sqrt{2}}{4}, \odot O$ 是 $\triangle A C D$ 的外接圆.
(1) 求 $B C$ 的长;
(2) 求 $\odot O$ 的半径.
某条城际铁路线共有 $A, B, C$ 三个车站, 每日上午均有两班次列车从 $A$ 站驶往 $C$ 站, 其中 $D 1001$ 次列车从 $A$ 站始发, 经停 $B$ 站后到达 $C$ 站, $G 1002$ 次列车从 $A$ 站始发, 直达 $C$ 站, 两个车次的列车在行驶过程中保持各自的行驶速度不变. 某校数学学习小组对列车运行情况进行研究, 收集到列车运行信息如下表所示.
列车运行时刻表
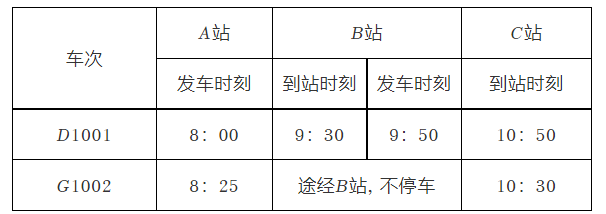
请根据表格中的信息, 解答下列问题:
(1) $D 1001$ 次列车从 $A$ 站到 $B$ 站行驶了 $\qquad$分钟, 从 $B$ 站到 $C$ 站行驶了 $\qquad$分钟;
(2) 记 $D 1001$ 次列车的行驶速度为 $v_1$, 离 $A$ 站的路程为 $d_1 ; G 1002$ 次列车的行驶速度为 $v_2$, 离 $A$ 站的路程为 $d_2$.
① $\frac{v_1}{v_2}=$ $\qquad$ .
② 从上午 8: 00 开始计时, 时长记为 $t$ 分钟 (如:上午 $9: 15$, 则 $t=75$ ), 已知 $v_1=240$ 千米/小时 (可换算为 4 千米/分钟),在 $G 10$ 02 次列车的行驶过程中 $(25 \leq t \leq 150)$, 若 $\left|d_1-d_2\right|=60$, 求 $t$ 的值.
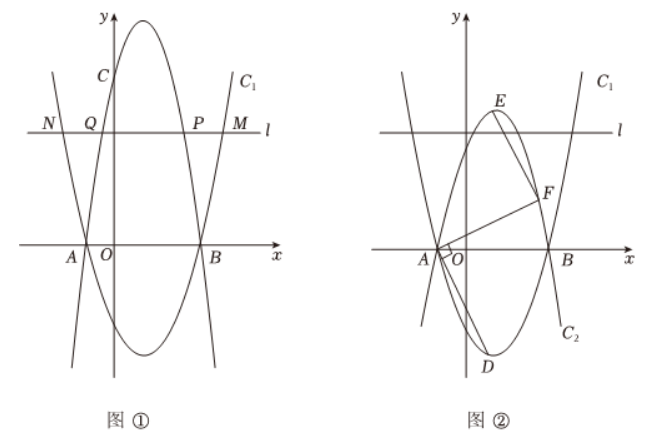
如图 ① , 二次函数 $y=x^2+b x+c$ 的图象 $C_1$ 与开口向下的二次函数图象 $C_2$ 均过点 $A(-1,0), B(3,0)$.
(1)求图象 $C_1$ 对应的函数表达式;
(2) 若图象 $C_2$ 过点 $C(0,6)$, 点 $P$ 位于第一象限, 且在图象 $C_2$ 上, 直线 $l$ 过点 $P$ 且与 $x$ 轴平行, 与图象 $C_2$ 的另一个交点为 $Q$ ( $Q$ 在 $P$左侧), 直线 $l$ 与图象 $C_1$ 的交点为 $M, N$ ( $N$ 在 $M$ 左侧). 当 $P Q=M P+Q N$ 时, 求点 $P$ 的坐标;
(3)如图 ② , $D, E$ 分别为二次函数图象 $C_1, C_2$ 的顶点, 连接 $A D$, 过点 $A$ 作 $A F \perp A D$, 交图象 $C_2$ 于点 $F$, 连接 $E F$, 当 $E F \| A D$ 时, 求图象 $C_2$ 对应的函数表达式.