如图 ① , 二次函数
(1)求图象
(2) 若图象
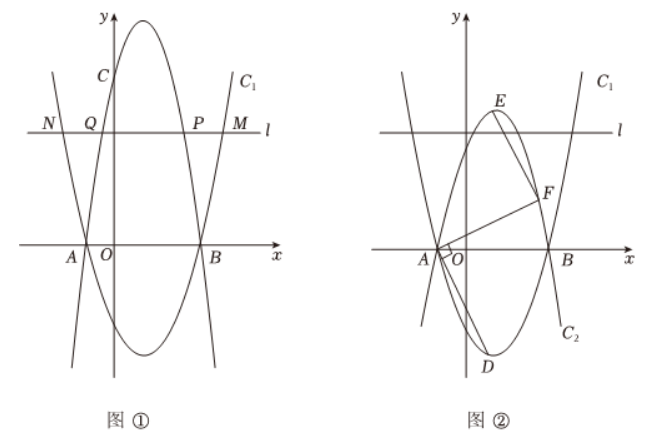
(3)如图 ② ,
(1)求图象
(2) 若图象
(3)如图 ② ,
